spotify-tracks-data-analysis
Spotify_Data_Track_Analysis
AvaniPatil, Sushma Akoju, Armana Anand 9/23/2021
Objective
Spotify is the worlds largest audio streaming application with services available in more than 175 countries. With a market share of approximately 32%, it has 365 million monthly active users, including 165 million paying subscribers, as of June 2021. A user can search for music based on a song, artist and genre album. They can create, share, edit playlists with other listeners all over the world. With such a massive user base, as one would imagine Spotify data is a gold mine for training machine learning algorithms and recommendation based systems. As a freemium service, Spotify implements multitudes of data learning tools and algorithms to leverage its data and create a streamlined experience for its users, unmatched by its competitors. Our objective with this project is to gain a deeper understanding of the Data Science discipline by accessing this data, and doing some preliminary analysis to come up with some conclusive observations.
We will primarily focus and attempt to understand each of the features, their technical definitions cited here https://developer.spotify.com/documentation/web-api/reference/#endpoint-get-audio-features . And we would like to see how existing human notions about music fare against what data actually tells us about. For example, it has been widely popular that the C# chord is most popular in western music. We want to find out how the features contribute to popularity.
Organization of the Report
- Objective
- Methodology
- Web Data Collection
- Pre-processing
- Analysis and Visualizations
- Popularity of each genre
- Correlation Map
- Correlation coefficient for each feature
- Popularity for each key
- Correlation based on feature groups
- Spotify tracks by Genre in the US
- Data summary and density distribution for all Spotify features
- Permutation Importances
- Modeling the Data
- Linear Regression Modelling to predict popularity
- Linear Regression Modelling to check the linear fit
- Random Forest Regression Fit
- Potential Bias and Conclusion
Methodology
In this section, the process of data gathering and cleaning are discussed.
Web Data Collection
#Importing the data set
tracks <- read_csv("https://raw.githubusercontent.com/sushmaakoju/spotify-tracks-data-analysis/main/SpotifyFeatures.csv")
## Rows: 232725 Columns: 18
## -- Column specification --------------------------------------------------------
## Delimiter: ","
## chr (7): genre, artist_name, track_name, track_id, key, mode, time_signature
## dbl (11): popularity, acousticness, danceability, duration_ms, energy, instr...
##
## i Use `spec()` to retrieve the full column specification for this data.
## i Specify the column types or set `show_col_types = FALSE` to quiet this message.
head(tracks,n=10)
## # A tibble: 10 x 18
## genre artist_name track_name track_id popularity acousticness danceability
## <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Movie Henri Salva~ C'est beau ~ 0BRjO6g~ 0 0.611 0.389
## 2 Movie Martin & le~ Perdu d'ava~ 0BjC1Nf~ 1 0.246 0.59
## 3 Movie Joseph Will~ Don't Let M~ 0CoSDzo~ 3 0.952 0.663
## 4 Movie Henri Salva~ Dis-moi Mon~ 0Gc6TVm~ 0 0.703 0.24
## 5 Movie Fabien Nataf Ouverture 0IuslXp~ 4 0.95 0.331
## 6 Movie Henri Salva~ Le petit so~ 0Mf1jKa~ 0 0.749 0.578
## 7 Movie Martin & le~ Premières r~ 0NUiKYR~ 2 0.344 0.703
## 8 Movie Laura Mayne Let Me Let ~ 0PbIF9Y~ 15 0.939 0.416
## 9 Movie Chorus Helka 0ST6uPf~ 0 0.00104 0.734
## 10 Movie Le Club des~ Les bisous ~ 0VSqZ3K~ 10 0.319 0.598
## # ... with 11 more variables: duration_ms <dbl>, energy <dbl>,
## # instrumentalness <dbl>, key <chr>, liveness <dbl>, loudness <dbl>,
## # mode <chr>, speechiness <dbl>, tempo <dbl>, time_signature <chr>,
## # valence <dbl>
colnames(tracks)
## [1] "genre" "artist_name" "track_name" "track_id"
## [5] "popularity" "acousticness" "danceability" "duration_ms"
## [9] "energy" "instrumentalness" "key" "liveness"
## [13] "loudness" "mode" "speechiness" "tempo"
## [17] "time_signature" "valence"
Armana Anand Code
Downloaded from Kaggle, this data was originally sourced from Spotify using their API.
Here is the link to the Kaggle dataset.
The data set consists of the features of around 200k top songs—Worldwide. Ranked by a proprietary algorithm for popularity in 2019.
Here are the features which will be measured to evaluate the data.
- Genre
- Artist_name
- Track_name
- Track_id
- Popularity: Scaled scaled from 0-100(Least –Most Popular)
- Acousticness: Measure of how acoustic the track is. Ranges from 0.0 to 1.0
- Danceability: Measured using a mixture of song features such as beat strength, tempo stability, and overall tempo.
- Duration_ms
- Energy: Measure from 0.0 to 1.0 and represents a perceptual measure of intensity and activity. Typically, energetic tracks feel fast, loud, and noisy.
- Instrumentalness: Does it contain vocals? Range 0-1.
- Key
- Liveness: Detects the presence of an audience in the recording.
- Loudness: Overall loudness of a track in decibels (dB). Values range between -55 and 5 dB.
- Mode
- Speechiness: Detects the presence of spoken words in a track.
- Tempo: Overall estimated tempo of a track in beats per minute (BPM).
- Time_signature
- Valence: Measure from 0.0 to 1.0 describing the musical positiveness conveyed by a track
More in depth information on how Spotify tags and analyses these features can be found here
Pre-processing
Let’s check for missing values in our data set.
#checking for missing values in the data set
colSums(is.na(tracks))
## genre artist_name track_name track_id
## 0 0 0 0
## popularity acousticness danceability duration_ms
## 0 0 0 0
## energy instrumentalness key liveness
## 0 0 0 0
## loudness mode speechiness tempo
## 0 0 0 0
## time_signature valence
## 0 0
As per above summary, there are no missing values in this data set.
# As there are no missing values, we will check for other errors.
# Let's check for distinct genre names to see if any genre is repeated.
distinct(data.frame(tracks$genre))
## tracks.genre
## 1 Movie
## 2 R&B
## 3 A Capella
## 4 Alternative
## 5 Country
## 6 Dance
## 7 Electronic
## 8 Anime
## 9 Folk
## 10 Blues
## 11 Opera
## 12 Hip-Hop
## 13 Children's Music
## 14 Children’s Music
## 15 Rap
## 16 Indie
## 17 Classical
## 18 Pop
## 19 Reggae
## 20 Reggaeton
## 21 Jazz
## 22 Rock
## 23 Ska
## 24 Comedy
## 25 Soul
## 26 Soundtrack
## 27 World
As we can see there are two Children’s Music genre. We should rectify this typo so that a single genre is visible.
# Rectifying typo in genre name Children's Music.
colnames(tracks)[colnames(tracks$genre) == "Children's Music"] <- "Children’s Music"
# Rechecking the distinct values.
distinct(data.frame(tracks$genre))
## tracks.genre
## 1 Movie
## 2 R&B
## 3 A Capella
## 4 Alternative
## 5 Country
## 6 Dance
## 7 Electronic
## 8 Anime
## 9 Folk
## 10 Blues
## 11 Opera
## 12 Hip-Hop
## 13 Children's Music
## 14 Children’s Music
## 15 Rap
## 16 Indie
## 17 Classical
## 18 Pop
## 19 Reggae
## 20 Reggaeton
## 21 Jazz
## 22 Rock
## 23 Ska
## 24 Comedy
## 25 Soul
## 26 Soundtrack
## 27 World
#Mutate variables from numeric to factor
tracks <- tracks %>%
mutate(genre = as.factor(genre),
key = as.factor(key),
genre = as.factor(str_replace_all(genre, "[[:punct:]]", "")),
mode = as.factor(mode))
summary(tracks)
## genre artist_name track_name
## Childrens Music: 14756 Length:232725 Length:232725
## Comedy : 9681 Class :character Class :character
## Soundtrack : 9646 Mode :character Mode :character
## Indie : 9543
## Jazz : 9441
## Pop : 9386
## (Other) :170272
## track_id popularity acousticness danceability
## Length:232725 Min. : 0.00 Min. :0.0000 Min. :0.0569
## Class :character 1st Qu.: 29.00 1st Qu.:0.0376 1st Qu.:0.4350
## Mode :character Median : 43.00 Median :0.2320 Median :0.5710
## Mean : 41.13 Mean :0.3686 Mean :0.5544
## 3rd Qu.: 55.00 3rd Qu.:0.7220 3rd Qu.:0.6920
## Max. :100.00 Max. :0.9960 Max. :0.9890
##
## duration_ms energy instrumentalness key
## Min. : 15387 Min. :0.0000203 Min. :0.0000000 C :27583
## 1st Qu.: 182857 1st Qu.:0.3850000 1st Qu.:0.0000000 G :26390
## Median : 220427 Median :0.6050000 Median :0.0000443 D :24077
## Mean : 235122 Mean :0.5709577 Mean :0.1483012 C# :23201
## 3rd Qu.: 265768 3rd Qu.:0.7870000 3rd Qu.:0.0358000 A :22671
## Max. :5552917 Max. :0.9990000 Max. :0.9990000 F :20279
## (Other):88524
## liveness loudness mode speechiness
## Min. :0.00967 Min. :-52.457 Major:151744 Min. :0.0222
## 1st Qu.:0.09740 1st Qu.:-11.771 Minor: 80981 1st Qu.:0.0367
## Median :0.12800 Median : -7.762 Median :0.0501
## Mean :0.21501 Mean : -9.570 Mean :0.1208
## 3rd Qu.:0.26400 3rd Qu.: -5.501 3rd Qu.:0.1050
## Max. :1.00000 Max. : 3.744 Max. :0.9670
##
## tempo time_signature valence
## Min. : 30.38 Length:232725 Min. :0.0000
## 1st Qu.: 92.96 Class :character 1st Qu.:0.2370
## Median :115.78 Mode :character Median :0.4440
## Mean :117.67 Mean :0.4549
## 3rd Qu.:139.05 3rd Qu.:0.6600
## Max. :242.90 Max. :1.0000
##
# Filter columns that are not presently needed for our analysis
tracks1 <- tracks %>% select(-c(track_id,time_signature))
# Glimpse data
glimpse(tracks1)
## Rows: 232,725
## Columns: 16
## $ genre <fct> Movie, Movie, Movie, Movie, Movie, Movie, Movie, Movi~
## $ artist_name <chr> "Henri Salvador", "Martin & les fées", "Joseph Willia~
## $ track_name <chr> "C'est beau de faire un Show", "Perdu d'avance (par G~
## $ popularity <dbl> 0, 1, 3, 0, 4, 0, 2, 15, 0, 10, 0, 2, 4, 3, 0, 0, 0, ~
## $ acousticness <dbl> 0.61100, 0.24600, 0.95200, 0.70300, 0.95000, 0.74900,~
## $ danceability <dbl> 0.389, 0.590, 0.663, 0.240, 0.331, 0.578, 0.703, 0.41~
## $ duration_ms <dbl> 99373, 137373, 170267, 152427, 82625, 160627, 212293,~
## $ energy <dbl> 0.9100, 0.7370, 0.1310, 0.3260, 0.2250, 0.0948, 0.270~
## $ instrumentalness <dbl> 0.00000000, 0.00000000, 0.00000000, 0.00000000, 0.123~
## $ key <fct> C#, F#, C, C#, F, C#, C#, F#, C, G, E, C, F#, D#, G, ~
## $ liveness <dbl> 0.3460, 0.1510, 0.1030, 0.0985, 0.2020, 0.1070, 0.105~
## $ loudness <dbl> -1.828, -5.559, -13.879, -12.178, -21.150, -14.970, -~
## $ mode <fct> Major, Minor, Minor, Major, Major, Major, Major, Majo~
## $ speechiness <dbl> 0.0525, 0.0868, 0.0362, 0.0395, 0.0456, 0.1430, 0.953~
## $ tempo <dbl> 166.969, 174.003, 99.488, 171.758, 140.576, 87.479, 8~
## $ valence <dbl> 0.8140, 0.8160, 0.3680, 0.2270, 0.3900, 0.3580, 0.533~
Before we can move to visualizations and deeper analysis, lets take a look at what the overall trend of our data is.
spotify_hist <- tracks[,-c(1,2,3,4,5,11,17)]
plot_num(spotify_hist)
## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.
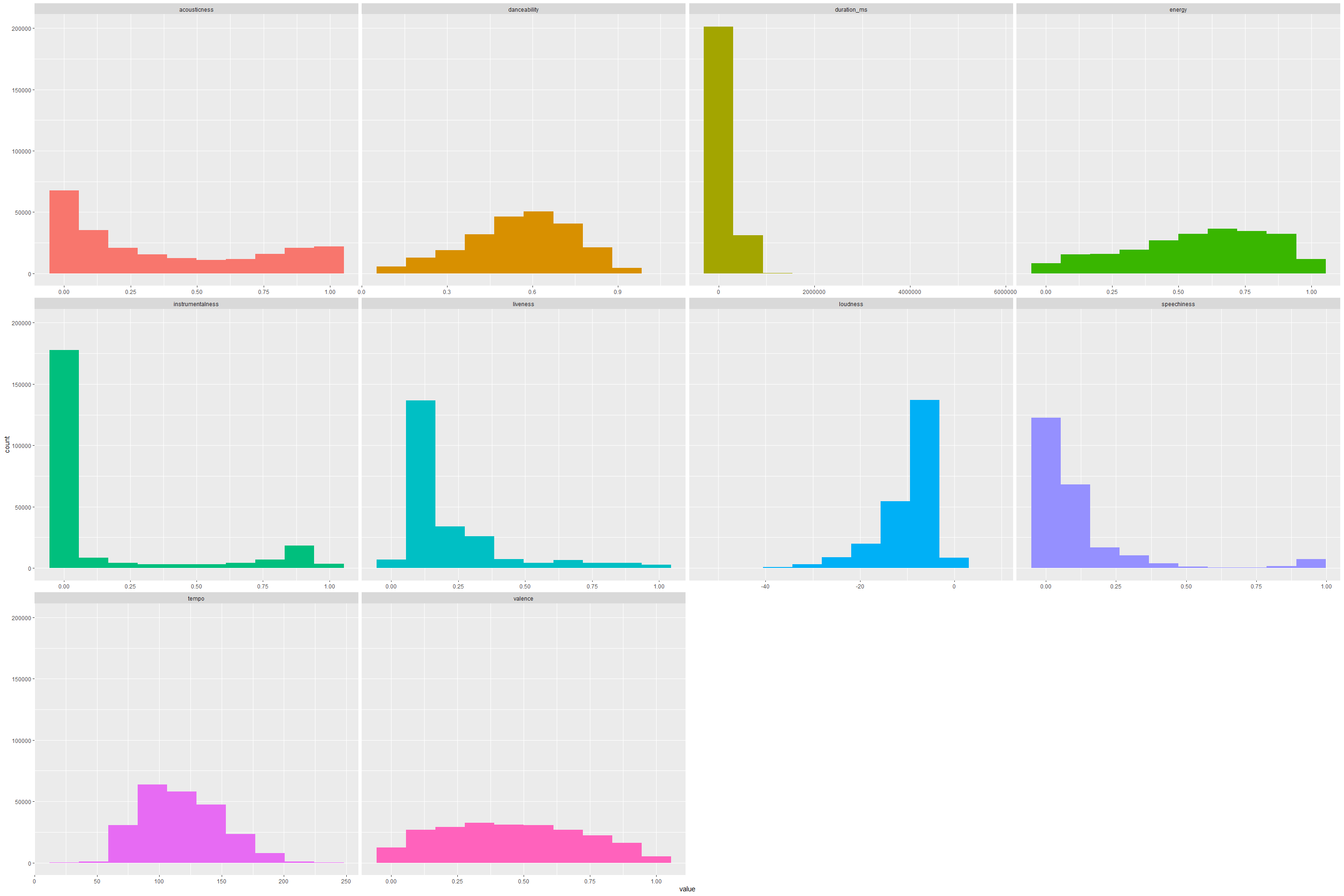
From the above it is interesting to note that danceability has a pretty normal distribution of songs in our dataset. To no surprise, there are not many people listening to Bach or YoYo Ma renditions of Vivaldi off late. We can clearly see the evidence of that by looking at the tall peak that signifies the clustering of most of our songs on the low to zero instrumental scale. Similarly, majority of the popular songs generally are 2- 5 mins long.
Analysis and Visualizations
Now that we have pre-processed our data set, we can visualize basic data to find correlations among our variables.
From our data set, we can group our data set by genre and focus on the popularity parameter for visualization of data.
genre_popularity <- tracks %>% select(popularity, genre) %>% group_by(genre) %>% summarise("average_popularity" = round(mean(popularity)))
p <- ggplot(data=genre_popularity, mapping = aes(x = reorder(genre,average_popularity), y = average_popularity, fill = genre)) +
geom_col() +
coord_flip() +
theme_minimal() +
theme(
legend.position = "none",
) +
labs(
y = "Average popularity",
x = "Genre"
)
p
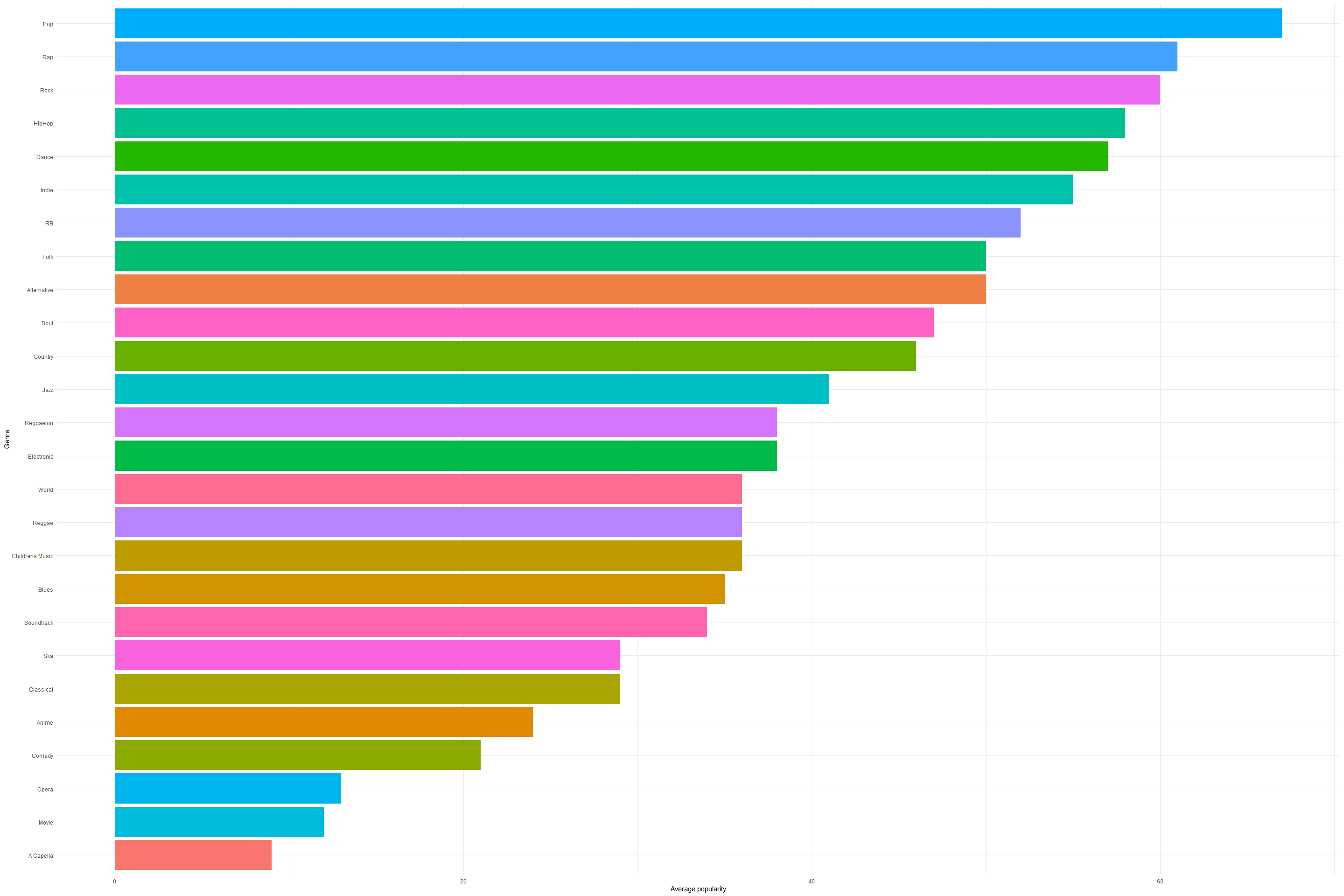
We have plotted the music genre from highest popularity to lowest
popularity.
We can see that the Top 5 popular genres on spotify are -
- Pop
- Rap
- Rock
- HipHop
- Dance
Genres with lowest popularity on spotify.
- Anime
- Comedy
- Opera
- Movie
- A Capella
Let’s analyse the relationship between all numeric Spotify features now using a correlation map.
# Plotting a correlation heat map to check correlation between all audio features.
ggcorr(tracks, low = "blue", high = "red")
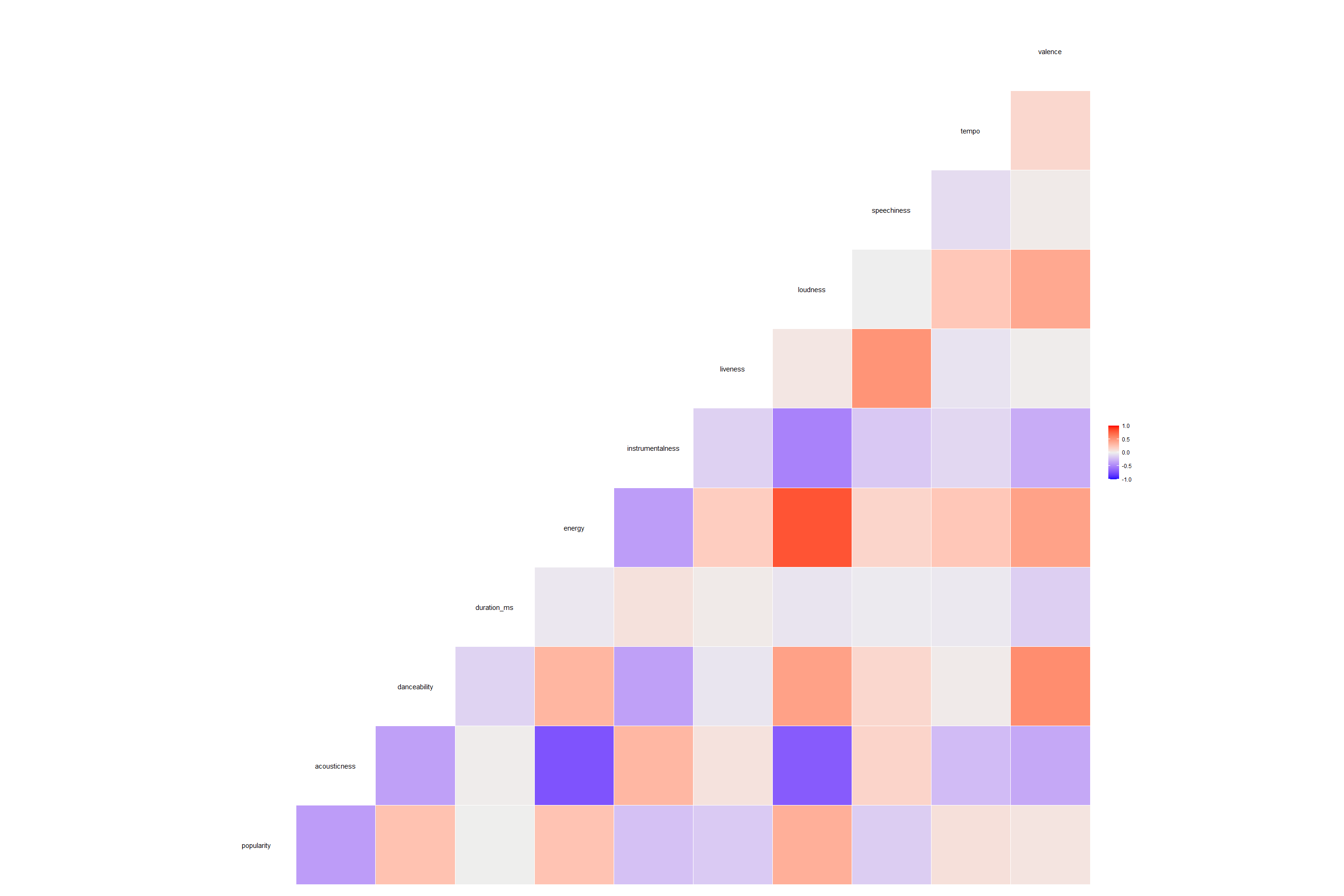
From above graph we can list out below significant observations -
-
Energy and loudness have the highest correlation.
-
Energy and acousticness have a highly-correlated inverse relationship
-
Loudness and acousticness have a highly-correlated inverse relationship
-
Some of the variables most correlated to Popularity seem to be: acousticness, danceability, energy, instrumentalness, and loudness.
Avani Patil Code
Now that we are familiar with the data set attributes and the objective of our analysis, let’s check for missing values in our data set.
# Checking for missing values in the data set
colSums(is.na(tracks))
## genre artist_name track_name track_id
## 0 0 0 0
## popularity acousticness danceability duration_ms
## 0 0 0 0
## energy instrumentalness key liveness
## 0 0 0 0
## loudness mode speechiness tempo
## 0 0 0 0
## time_signature valence
## 0 0
As per above summary, there are no missing values in this data set.
Now that we have the pre-processed data set, we can visualize basic data to find correlations among our variables.
In our data set, we will be focusing on Popularity as our dependent
variable.
So how is popularity actually calculated and what makes a song popular?
According to Spotify - popularity is calculated by an algorithm and is based, in the most part, on the total number of plays the track has had and how recently those tracks are played. Generally speaking, songs that are being played a lot now will have a higher popularity than songs that were played a lot in the past.
So for starters, let’s check the relationship between all the audio features of Spotify data set to try and find some correlation between them using th correlation heatmap mentioned above.
From above mentioned heatmap we can summarize that -
-
‘Energy’ and ‘loudness’ have the highest correlation, and a positive one, which is not very surprising as the louder a song is, the more energy it has.
-
‘Energy’ and ‘acousticness’ have a highly-correlated inverse relationship, which also makes total sense. The more a song skews towards being acoustic, the less energy value it tends to have.
We noticed similar inverse relationship between ‘Loudness’ and ‘acousticness’ as well.
Let’s sort the the data by popularity to check the top 10 popular songs.
tracks1 %>% top_n(10,popularity) %>% select(artist_name, track_name, popularity) %>% arrange(desc(popularity))
## # A tibble: 19 x 3
## artist_name track_name popularity
## <chr> <chr> <dbl>
## 1 Ariana Grande 7 rings 100
## 2 Ariana Grande 7 rings 100
## 3 Ariana Grande break up with your girlfriend, i'm bored 99
## 4 Post Malone Wow. 99
## 5 Ariana Grande break up with your girlfriend, i'm bored 99
## 6 Post Malone Wow. 99
## 7 Daddy Yankee Con Calma 98
## 8 Daddy Yankee Con Calma 98
## 9 Daddy Yankee Con Calma 98
## 10 Halsey Without Me 97
## 11 Ava Max Sweet but Psycho 97
## 12 Post Malone Sunflower - Spider-Man: Into the Spider-Verse 97
## 13 Halsey Without Me 97
## 14 Post Malone Sunflower - Spider-Man: Into the Spider-Verse 97
## 15 Halsey Without Me 97
## 16 Sam Smith Dancing With A Stranger (with Normani) 97
## 17 Marshmello Happier 97
## 18 Ava Max Sweet but Psycho 97
## 19 Pedro Capó Calma - Remix 97
Correlation coefficient for each feature
Now that we have plotted the correlation heat map, let’s check the correlation coefficient values against each relationship.
# Eliminate the parameters which are not relevant to our correlation analysis and copy the same in a new df.
tracks2 <- tracks %>% select(-c(track_id,time_signature,key,mode))
cor(tracks2[,4:14])
## popularity acousticness danceability duration_ms energy
## popularity 1.00000000 -0.38129531 0.25656447 0.00234802 0.24892177
## acousticness -0.38129531 1.00000000 -0.36454559 0.01120296 -0.72557636
## danceability 0.25656447 -0.36454559 1.00000000 -0.12578071 0.32580699
## duration_ms 0.00234802 0.01120296 -0.12578071 1.00000000 -0.03054981
## energy 0.24892177 -0.72557636 0.32580699 -0.03054981 1.00000000
## instrumentalness -0.21098311 0.31615411 -0.36494121 0.07602064 -0.37895695
## liveness -0.16799519 0.06900353 -0.04168384 0.02378262 0.19280086
## loudness 0.36301074 -0.69020168 0.43866848 -0.04761783 0.81608797
## speechiness -0.15107582 0.15093494 0.13455996 -0.01617141 0.14511980
## tempo 0.08103891 -0.23824736 0.02193911 -0.02845610 0.22877413
## valence 0.06007629 -0.32579820 0.54715402 -0.14181119 0.43677118
## instrumentalness liveness loudness speechiness
## popularity -0.21098311 -0.16799519 0.363010736 -0.151075818
## acousticness 0.31615411 0.06900353 -0.690201678 0.150934938
## danceability -0.36494121 -0.04168384 0.438668484 0.134559958
## duration_ms 0.07602064 0.02378262 -0.047617826 -0.016171409
## energy -0.37895695 0.19280086 0.816087967 0.145119802
## instrumentalness 1.00000000 -0.13419771 -0.506320170 -0.177147448
## liveness -0.13419771 1.00000000 0.045685710 0.510146517
## loudness -0.50632017 0.04568571 1.000000000 -0.002272769
## speechiness -0.17714745 0.51014652 -0.002272769 1.000000000
## tempo -0.10413303 -0.05135460 0.228363652 -0.081540541
## valence -0.30752185 0.01180437 0.399901355 0.023841622
## tempo valence
## popularity 0.08103891 0.06007629
## acousticness -0.23824736 -0.32579820
## danceability 0.02193911 0.54715402
## duration_ms -0.02845610 -0.14181119
## energy 0.22877413 0.43677118
## instrumentalness -0.10413303 -0.30752185
## liveness -0.05135460 0.01180437
## loudness 0.22836365 0.39990136
## speechiness -0.08154054 0.02384162
## tempo 1.00000000 0.13485723
## valence 0.13485723 1.00000000
With our dependent variable being ‘popularity’, from above graph we can
note that there are poor correlation values across most of our
independent variables.
From this correlation matrix, we can pluck five of the best features
(ones with the highest correlation) to use later on as predictors while
training our model -
acousticness,
danceability,
energy,
instrumentalness, and
loudness.
Popularity for each key
Now let’s compare Popularity with Key and check if we can find any significant relationship between these two attributes.
So when it comes to western music, there are 12 keys. Let’s check the popularity for each and every key.
# Plot keys and their popularity values.
tracks %>% group_by(key) %>% select(key, popularity) %>%
ggplot(aes(x=as.factor(key),y=popularity,fill=as.factor(key))) +
geom_boxplot() + theme(legend.position = "none") +
labs(title="Popularity of Song Keys",
x="Key", y="Popularity")
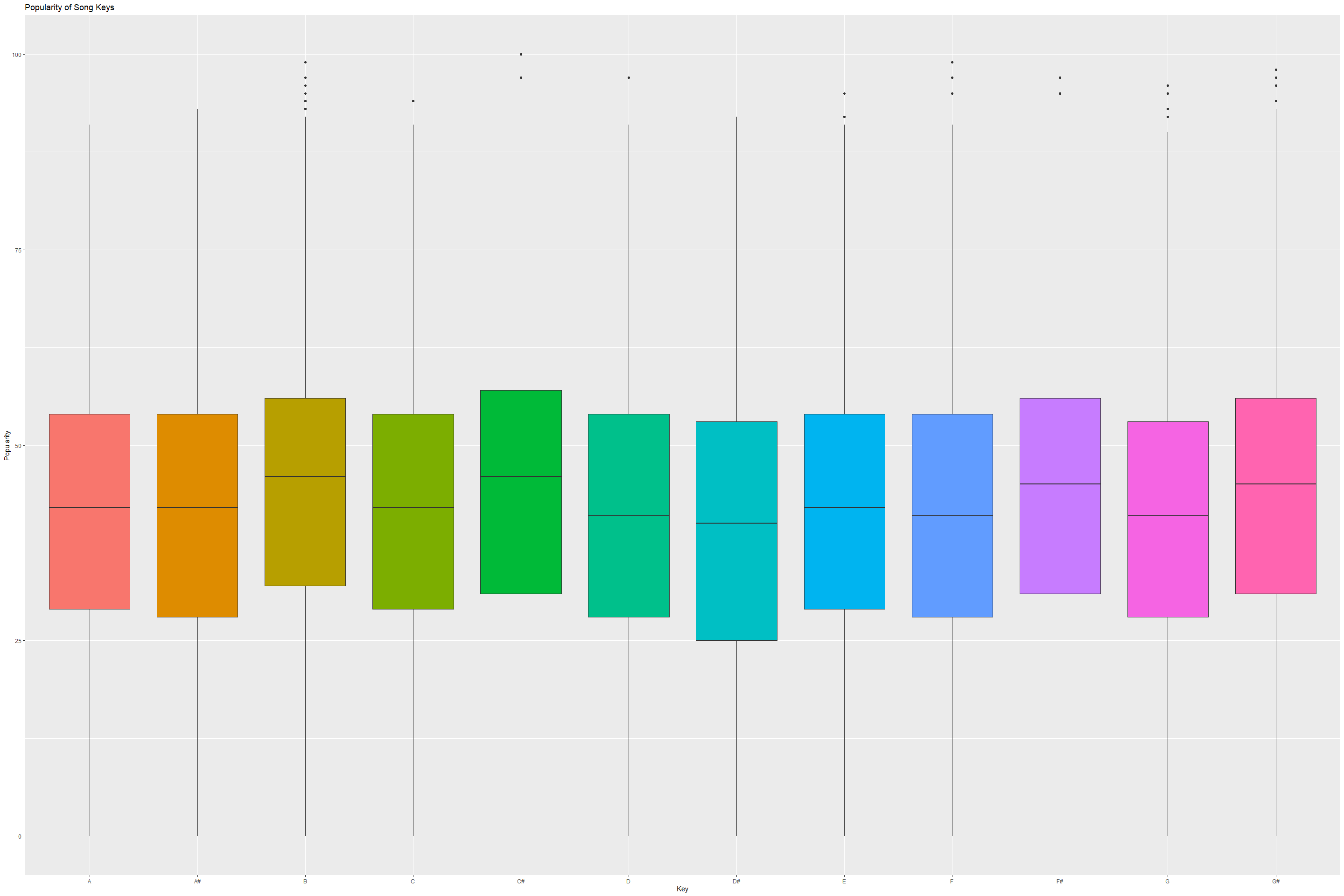
There seems to be little differentiation between the keys and popularity. However, one key does seem to have a larger number of popular songs in it - C-Sharp key.
We can check this by filtering out songs where popularity is above 70 on a scale on 100 and check how many popular songs fall under this key.
#tracks %>% filter(popularity > 70) %>% group_by(key) %>% summarize(count = n()) %>% arrange(desc(count))
Key 1 (which applies to c-Sharp) has more popular songs (1068 songs) than other keys. This could be a potential predictor variable, so we will encode a new binary variable we can use in our model.
# Creating a new binary variable for key attribute
tracks$isKey1 <- as.integer(tracks$key == 1)
Linear Regression Modelling
To warm-up, we will be starting with a simple linear regression model and try and manipulate the predictor attributes to find the a model with lowest Residual standard error and highest Adjusted R-squared.
Linear Model 1 (m1):
Dependent Variable - Popularity
Predictor Variables - acousticness danceability, energy,
instrumentalness, liveness, loudness, speechiness, tempo, valence,
isKey1, energy and loudness.
m1 <- lm(popularity ~ acousticness + danceability + energy + instrumentalness + liveness + loudness + speechiness + tempo + valence + isKey1 + (energy * loudness), data=tracks)
summary(m1)
##
## Call:
## lm(formula = popularity ~ acousticness + danceability + energy +
## instrumentalness + liveness + loudness + speechiness + tempo +
## valence + isKey1 + (energy * loudness), data = tracks)
##
## Residuals:
## Min 1Q Median 3Q Max
## -58.073 -10.190 1.449 11.049 56.127
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 55.786296 0.336716 165.678 < 0.0000000000000002 ***
## acousticness -12.008112 0.154651 -77.647 < 0.0000000000000002 ***
## danceability 17.896007 0.244464 73.205 < 0.0000000000000002 ***
## energy -4.695025 0.304857 -15.401 < 0.0000000000000002 ***
## instrumentalness -4.247604 0.133015 -31.933 < 0.0000000000000002 ***
## liveness -9.481621 0.201964 -46.947 < 0.0000000000000002 ***
## loudness 0.683820 0.012004 56.967 < 0.0000000000000002 ***
## speechiness -7.807189 0.233538 -33.430 < 0.0000000000000002 ***
## tempo -0.004373 0.001118 -3.912 0.0000915725170060 ***
## valence -13.297562 0.165468 -80.363 < 0.0000000000000002 ***
## isKey1 NA NA NA NA
## energy:loudness 0.180617 0.023932 7.547 0.0000000000000447 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.92 on 232714 degrees of freedom
## Multiple R-squared: 0.2339, Adjusted R-squared: 0.2338
## F-statistic: 7104 on 10 and 232714 DF, p-value: < 0.00000000000000022
From above model, we can observe that the Adjusted R-squared is very low
and the Residual standard error is on the higher end for this model.
Also, the key attribute is not adding up to anything in our model.
In our next modelling attempt, let’s get rid of the key attribute and add couple of more parameters which have shown correlation among them.
Linear Model 2 (m2):
Dependent Variable - Popularity
Predictor Variables - acousticness danceability, energy,
instrumentalness, liveness, loudness, speechiness, tempo, valence,
energy and loudness, acousticness and instrumentalness.
In this model, we have added an additional predictor acousticness and instrumentalness.
m2 <- lm(popularity ~ acousticness + danceability + energy + instrumentalness + liveness + loudness + speechiness + tempo + valence + (energy * loudness) + (acousticness * instrumentalness), data=tracks)
summary(m2)
##
## Call:
## lm(formula = popularity ~ acousticness + danceability + energy +
## instrumentalness + liveness + loudness + speechiness + tempo +
## valence + (energy * loudness) + (acousticness * instrumentalness),
## data = tracks)
##
## Residuals:
## Min 1Q Median 3Q Max
## -58.721 -9.951 1.316 10.908 56.072
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 58.290825 0.336710 173.119
## acousticness -15.002658 0.161330 -92.994
## danceability 18.052361 0.242599 74.412
## energy -7.971595 0.307375 -25.934
## instrumentalness -14.202184 0.211638 -67.106
## liveness -8.856882 0.200681 -44.134
## loudness 0.867896 0.012298 70.572
## speechiness -7.403721 0.231840 -31.935
## tempo -0.003738 0.001109 -3.369
## valence -13.573857 0.164261 -82.636
## energy:loudness -0.252460 0.024815 -10.174
## acousticness:instrumentalness 18.970531 0.315269 60.173
## Pr(>|t|)
## (Intercept) < 0.0000000000000002 ***
## acousticness < 0.0000000000000002 ***
## danceability < 0.0000000000000002 ***
## energy < 0.0000000000000002 ***
## instrumentalness < 0.0000000000000002 ***
## liveness < 0.0000000000000002 ***
## loudness < 0.0000000000000002 ***
## speechiness < 0.0000000000000002 ***
## tempo 0.000755 ***
## valence < 0.0000000000000002 ***
## energy:loudness < 0.0000000000000002 ***
## acousticness:instrumentalness < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.8 on 232713 degrees of freedom
## Multiple R-squared: 0.2456, Adjusted R-squared: 0.2456
## F-statistic: 6888 on 11 and 232713 DF, p-value: < 0.00000000000000022
In above model, we can see that the Adjusted R-squared is has increased
from 0.2338 to 0.2456 and the Residual standard error has decreased from
15.92 to 15.8.
However, the updated Adjusted R-squared is still quite low.
Let’s try and improve the model further by adding for correlation predictors.
Linear Model 3 (m3):
Dependent Variable - Popularity
Predictor Variables - acousticness danceability, energy,
instrumentalness, liveness, loudness, speechiness, tempo, valence,
energy and loudness, acousticness and instrumentalness, energy and
danceability.
In this model, we have added an additional predictor energy and danceability.
m3 <- lm(popularity ~ acousticness + danceability + energy + instrumentalness + liveness + loudness + speechiness + tempo + valence + (energy * loudness) + (acousticness * instrumentalness) + (energy * danceability), data=tracks)
summary(m3)
##
## Call:
## lm(formula = popularity ~ acousticness + danceability + energy +
## instrumentalness + liveness + loudness + speechiness + tempo +
## valence + (energy * loudness) + (acousticness * instrumentalness) +
## (energy * danceability), data = tracks)
##
## Residuals:
## Min 1Q Median 3Q Max
## -59.368 -9.970 1.293 10.917 56.801
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 62.3343933 0.4171325 149.435
## acousticness -15.1516901 0.1614924 -93.823
## danceability 11.0487426 0.4909714 22.504
## energy -16.0219339 0.5789554 -27.674
## instrumentalness -14.1442256 0.2115453 -66.861
## liveness -8.7826321 0.2006162 -43.778
## loudness 0.9388640 0.0130301 72.053
## speechiness -7.1087332 0.2324033 -30.588
## tempo -0.0009986 0.0011213 -0.891
## valence -13.5071933 0.1642163 -82.252
## energy:loudness -0.3752865 0.0259063 -14.486
## acousticness:instrumentalness 18.5180796 0.3162925 58.547
## danceability:energy 12.8862781 0.7855224 16.405
## Pr(>|t|)
## (Intercept) <0.0000000000000002 ***
## acousticness <0.0000000000000002 ***
## danceability <0.0000000000000002 ***
## energy <0.0000000000000002 ***
## instrumentalness <0.0000000000000002 ***
## liveness <0.0000000000000002 ***
## loudness <0.0000000000000002 ***
## speechiness <0.0000000000000002 ***
## tempo 0.373
## valence <0.0000000000000002 ***
## energy:loudness <0.0000000000000002 ***
## acousticness:instrumentalness <0.0000000000000002 ***
## danceability:energy <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.79 on 232712 degrees of freedom
## Multiple R-squared: 0.2465, Adjusted R-squared: 0.2464
## F-statistic: 6344 on 12 and 232712 DF, p-value: < 0.00000000000000022
In above model, we can see that the Adjusted R-squared is has increased from 0.2456 to 0.2464 and the Residual standard error has decreased from 15.8 to 15.79.
We’ll chose the model m3 as it has the best fit (R-Squared) to the data compared to other models.
Let’s plot model m3 using residual plot and QQ plot.
# Plotting residual plot for Model 3
am3 <- augment(m3)
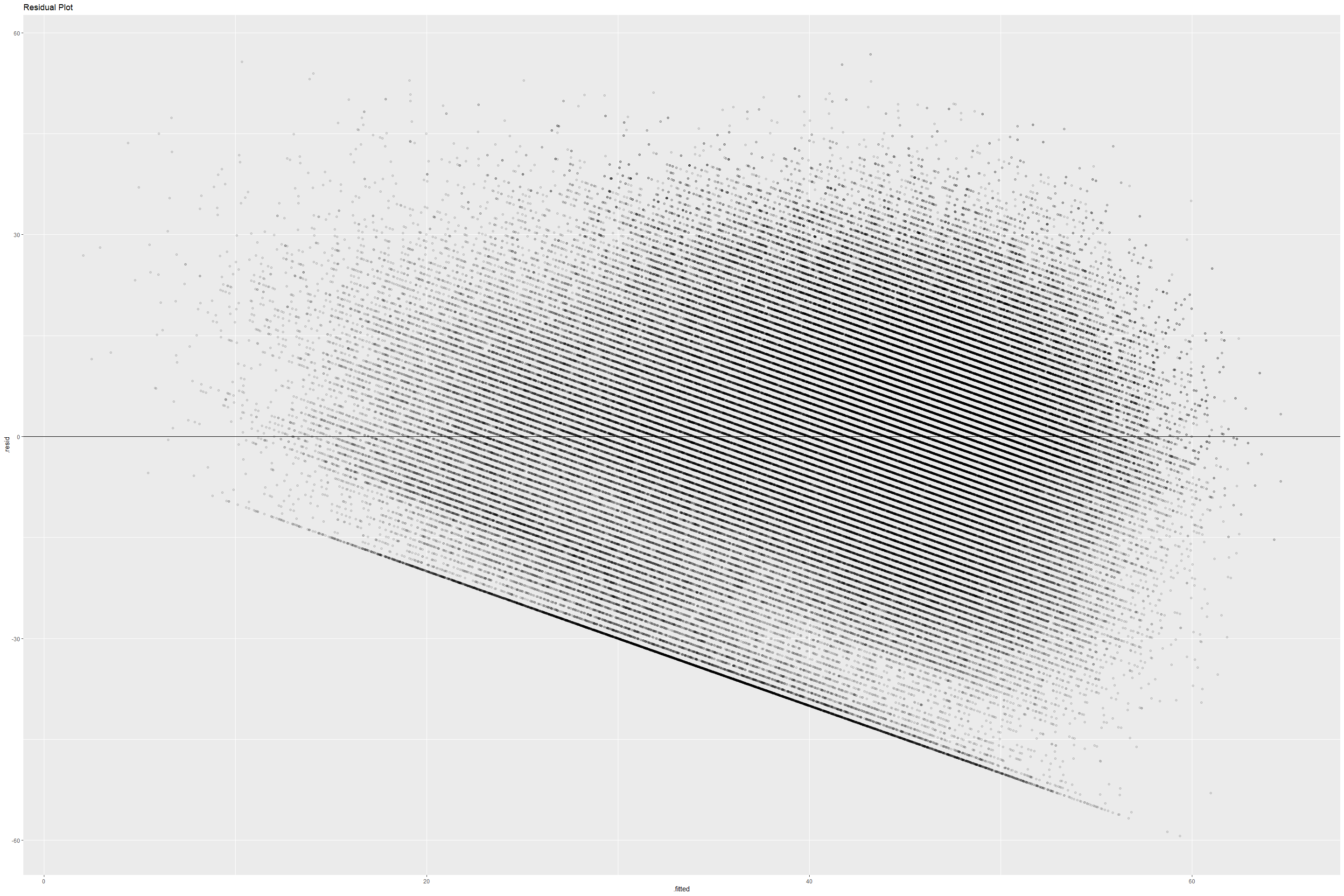
am3 %>% ggplot(aes(x=.fitted,y=.resid)) +
geom_point(alpha=0.1) + geom_hline(yintercept=0) +
labs(title="Residual Plot")
# Plotting QQ plot for Model 3
am3 %>% ggplot(aes(sample=.std.resid)) +
geom_qq() + geom_qq_line() +
labs(title="QQ Plot")
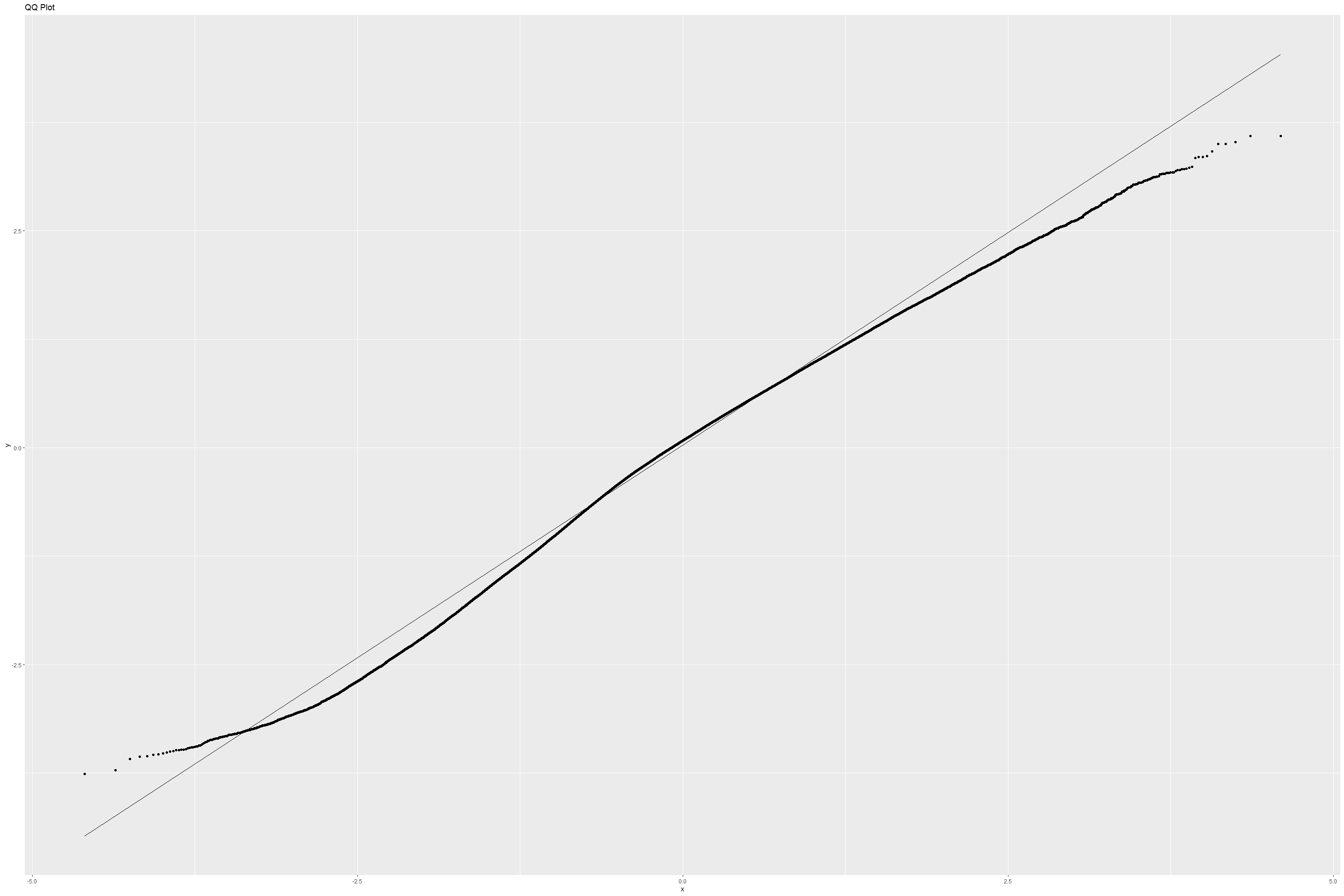
The residual plot has a definite pattern however, the QQ plot shows that our residuals aren’t exactly normal throughout the range of samples.
Given the low Adjusted R-squared, and unusual patterns in the residuals, the models we’ve created seem like they are unsuitable for predicting a song’s popularity on Spotify.
Sushma Akoju Code
Goal :
We primarily focus and attempt to understand each of the features, their
technical definitions cited here
https://developer.spotify.com/documentation/web-api/reference/#endpoint-get-audio-features
. we would like to see how existing human notions about music fare
against what data actually tells us about. For example, it has been
widely popular that the C# chord is most popular in western music. We
want to find out how the features contribute to popularity.
Example: “My favorite things” song from “The Sound of music” movie which was very popular back in 1960s and still considered a classic is unfortunately has a popularity score of zero while a modern, contemporary version inspired from the same song and rewritten with different lyrics and named as “7 rings” by Ariana Grande, has a popularity score of 100.
check few quick summaries for dataframe
head(tracks)
## # A tibble: 6 x 19
## genre artist_name track_name track_id popularity acousticness danceability
## <fct> <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Movie Henri Salva~ C'est beau ~ 0BRjO6ga~ 0 0.611 0.389
## 2 Movie Martin & le~ Perdu d'ava~ 0BjC1Nfo~ 1 0.246 0.59
## 3 Movie Joseph Will~ Don't Let M~ 0CoSDzoN~ 3 0.952 0.663
## 4 Movie Henri Salva~ Dis-moi Mon~ 0Gc6TVm5~ 0 0.703 0.24
## 5 Movie Fabien Nataf Ouverture 0IuslXpM~ 4 0.95 0.331
## 6 Movie Henri Salva~ Le petit so~ 0Mf1jKa8~ 0 0.749 0.578
## # ... with 12 more variables: duration_ms <dbl>, energy <dbl>,
## # instrumentalness <dbl>, key <fct>, liveness <dbl>, loudness <dbl>,
## # mode <fct>, speechiness <dbl>, tempo <dbl>, time_signature <chr>,
## # valence <dbl>, isKey1 <int>
colSums(is.na(tracks))
## genre artist_name track_name track_id
## 0 0 0 0
## popularity acousticness danceability duration_ms
## 0 0 0 0
## energy instrumentalness key liveness
## 0 0 0 0
## loudness mode speechiness tempo
## 0 0 0 0
## time_signature valence isKey1
## 0 0 0
head( tracks)
## # A tibble: 6 x 19
## genre artist_name track_name track_id popularity acousticness danceability
## <fct> <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Movie Henri Salva~ C'est beau ~ 0BRjO6ga~ 0 0.611 0.389
## 2 Movie Martin & le~ Perdu d'ava~ 0BjC1Nfo~ 1 0.246 0.59
## 3 Movie Joseph Will~ Don't Let M~ 0CoSDzoN~ 3 0.952 0.663
## 4 Movie Henri Salva~ Dis-moi Mon~ 0Gc6TVm5~ 0 0.703 0.24
## 5 Movie Fabien Nataf Ouverture 0IuslXpM~ 4 0.95 0.331
## 6 Movie Henri Salva~ Le petit so~ 0Mf1jKa8~ 0 0.749 0.578
## # ... with 12 more variables: duration_ms <dbl>, energy <dbl>,
## # instrumentalness <dbl>, key <fct>, liveness <dbl>, loudness <dbl>,
## # mode <fct>, speechiness <dbl>, tempo <dbl>, time_signature <chr>,
## # valence <dbl>, isKey1 <int>
glimpse(tracks)
## Rows: 232,725
## Columns: 19
## $ genre <fct> Movie, Movie, Movie, Movie, Movie, Movie, Movie, Movi~
## $ artist_name <chr> "Henri Salvador", "Martin & les fées", "Joseph Willia~
## $ track_name <chr> "C'est beau de faire un Show", "Perdu d'avance (par G~
## $ track_id <chr> "0BRjO6ga9RKCKjfDqeFgWV", "0BjC1NfoEOOusryehmNudP", "~
## $ popularity <dbl> 0, 1, 3, 0, 4, 0, 2, 15, 0, 10, 0, 2, 4, 3, 0, 0, 0, ~
## $ acousticness <dbl> 0.61100, 0.24600, 0.95200, 0.70300, 0.95000, 0.74900,~
## $ danceability <dbl> 0.389, 0.590, 0.663, 0.240, 0.331, 0.578, 0.703, 0.41~
## $ duration_ms <dbl> 99373, 137373, 170267, 152427, 82625, 160627, 212293,~
## $ energy <dbl> 0.9100, 0.7370, 0.1310, 0.3260, 0.2250, 0.0948, 0.270~
## $ instrumentalness <dbl> 0.00000000, 0.00000000, 0.00000000, 0.00000000, 0.123~
## $ key <fct> C#, F#, C, C#, F, C#, C#, F#, C, G, E, C, F#, D#, G, ~
## $ liveness <dbl> 0.3460, 0.1510, 0.1030, 0.0985, 0.2020, 0.1070, 0.105~
## $ loudness <dbl> -1.828, -5.559, -13.879, -12.178, -21.150, -14.970, -~
## $ mode <fct> Major, Minor, Minor, Major, Major, Major, Major, Majo~
## $ speechiness <dbl> 0.0525, 0.0868, 0.0362, 0.0395, 0.0456, 0.1430, 0.953~
## $ tempo <dbl> 166.969, 174.003, 99.488, 171.758, 140.576, 87.479, 8~
## $ time_signature <chr> "4/4", "4/4", "5/4", "4/4", "4/4", "4/4", "4/4", "4/4~
## $ valence <dbl> 0.8140, 0.8160, 0.3680, 0.2270, 0.3900, 0.3580, 0.533~
## $ isKey1 <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,~
Including Plots
Some genres are duplicated. (encoding mismatches).
na.omit(tracks)
## # A tibble: 232,725 x 19
## genre artist_name track_name track_id popularity acousticness danceability
## <fct> <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Movie Henri Salva~ C'est beau ~ 0BRjO6g~ 0 0.611 0.389
## 2 Movie Martin & le~ Perdu d'ava~ 0BjC1Nf~ 1 0.246 0.59
## 3 Movie Joseph Will~ Don't Let M~ 0CoSDzo~ 3 0.952 0.663
## 4 Movie Henri Salva~ Dis-moi Mon~ 0Gc6TVm~ 0 0.703 0.24
## 5 Movie Fabien Nataf Ouverture 0IuslXp~ 4 0.95 0.331
## 6 Movie Henri Salva~ Le petit so~ 0Mf1jKa~ 0 0.749 0.578
## 7 Movie Martin & le~ Premières r~ 0NUiKYR~ 2 0.344 0.703
## 8 Movie Laura Mayne Let Me Let ~ 0PbIF9Y~ 15 0.939 0.416
## 9 Movie Chorus Helka 0ST6uPf~ 0 0.00104 0.734
## 10 Movie Le Club des~ Les bisous ~ 0VSqZ3K~ 10 0.319 0.598
## # ... with 232,715 more rows, and 12 more variables: duration_ms <dbl>,
## # energy <dbl>, instrumentalness <dbl>, key <fct>, liveness <dbl>,
## # loudness <dbl>, mode <fct>, speechiness <dbl>, tempo <dbl>,
## # time_signature <chr>, valence <dbl>, isKey1 <int>
genres <- distinct(tracks, genre)$genre
genres
## [1] Movie RB A Capella Alternative
## [5] Country Dance Electronic Anime
## [9] Folk Blues Opera HipHop
## [13] Childrens Music Rap Indie Classical
## [17] Pop Reggae Reggaeton Jazz
## [21] Rock Ska Comedy Soul
## [25] Soundtrack World
## 26 Levels: A Capella Alternative Anime Blues Childrens Music ... World
tracks[!duplicated(tracks$track_id),]
## # A tibble: 176,774 x 19
## genre artist_name track_name track_id popularity acousticness danceability
## <fct> <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Movie Henri Salva~ C'est beau ~ 0BRjO6g~ 0 0.611 0.389
## 2 Movie Martin & le~ Perdu d'ava~ 0BjC1Nf~ 1 0.246 0.59
## 3 Movie Joseph Will~ Don't Let M~ 0CoSDzo~ 3 0.952 0.663
## 4 Movie Henri Salva~ Dis-moi Mon~ 0Gc6TVm~ 0 0.703 0.24
## 5 Movie Fabien Nataf Ouverture 0IuslXp~ 4 0.95 0.331
## 6 Movie Henri Salva~ Le petit so~ 0Mf1jKa~ 0 0.749 0.578
## 7 Movie Martin & le~ Premières r~ 0NUiKYR~ 2 0.344 0.703
## 8 Movie Laura Mayne Let Me Let ~ 0PbIF9Y~ 15 0.939 0.416
## 9 Movie Chorus Helka 0ST6uPf~ 0 0.00104 0.734
## 10 Movie Le Club des~ Les bisous ~ 0VSqZ3K~ 10 0.319 0.598
## # ... with 176,764 more rows, and 12 more variables: duration_ms <dbl>,
## # energy <dbl>, instrumentalness <dbl>, key <fct>, liveness <dbl>,
## # loudness <dbl>, mode <fct>, speechiness <dbl>, tempo <dbl>,
## # time_signature <chr>, valence <dbl>, isKey1 <int>
genres <- distinct(tracks, genre)$genre
Convert character format columns: key and mode to numeric values.
unique(tracks$key)
## [1] C# F# C F G E D# G# D A# A B
## Levels: A A# B C C# D D# E F F# G G#
unique(as.numeric(as.factor(tracks$key)))
## [1] 5 10 4 9 11 8 7 12 6 2 1 3
tracks$key <- as.numeric(as.factor(tracks$key))
unique(tracks$mode)
## [1] Major Minor
## Levels: Major Minor
unique(as.numeric(as.factor(tracks$mode)))
## [1] 1 2
tracks$mode <- as.numeric(as.factor(tracks$mode))
Get all numeric columns from the dataframe.
str(tracks)
## spec_tbl_df [232,725 x 19] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ genre : Factor w/ 26 levels "A Capella","Alternative",..: 15 15 15 15 15 15 15 15 15 15 ...
## $ artist_name : chr [1:232725] "Henri Salvador" "Martin & les fées" "Joseph Williams" "Henri Salvador" ...
## $ track_name : chr [1:232725] "C'est beau de faire un Show" "Perdu d'avance (par Gad Elmaleh)" "Don't Let Me Be Lonely Tonight" "Dis-moi Monsieur Gordon Cooper" ...
## $ track_id : chr [1:232725] "0BRjO6ga9RKCKjfDqeFgWV" "0BjC1NfoEOOusryehmNudP" "0CoSDzoNIKCRs124s9uTVy" "0Gc6TVm52BwZD07Ki6tIvf" ...
## $ popularity : num [1:232725] 0 1 3 0 4 0 2 15 0 10 ...
## $ acousticness : num [1:232725] 0.611 0.246 0.952 0.703 0.95 0.749 0.344 0.939 0.00104 0.319 ...
## $ danceability : num [1:232725] 0.389 0.59 0.663 0.24 0.331 0.578 0.703 0.416 0.734 0.598 ...
## $ duration_ms : num [1:232725] 99373 137373 170267 152427 82625 ...
## $ energy : num [1:232725] 0.91 0.737 0.131 0.326 0.225 0.0948 0.27 0.269 0.481 0.705 ...
## $ instrumentalness: num [1:232725] 0 0 0 0 0.123 0 0 0 0.00086 0.00125 ...
## $ key : num [1:232725] 5 10 4 5 9 5 5 10 4 11 ...
## $ liveness : num [1:232725] 0.346 0.151 0.103 0.0985 0.202 0.107 0.105 0.113 0.0765 0.349 ...
## $ loudness : num [1:232725] -1.83 -5.56 -13.88 -12.18 -21.15 ...
## $ mode : num [1:232725] 1 2 2 1 1 1 1 1 1 1 ...
## $ speechiness : num [1:232725] 0.0525 0.0868 0.0362 0.0395 0.0456 0.143 0.953 0.0286 0.046 0.0281 ...
## $ tempo : num [1:232725] 167 174 99.5 171.8 140.6 ...
## $ time_signature : chr [1:232725] "4/4" "4/4" "5/4" "4/4" ...
## $ valence : num [1:232725] 0.814 0.816 0.368 0.227 0.39 0.358 0.533 0.274 0.765 0.718 ...
## $ isKey1 : int [1:232725] 0 0 0 0 0 0 0 0 0 0 ...
## - attr(*, "spec")=
## .. cols(
## .. genre = col_character(),
## .. artist_name = col_character(),
## .. track_name = col_character(),
## .. track_id = col_character(),
## .. popularity = col_double(),
## .. acousticness = col_double(),
## .. danceability = col_double(),
## .. duration_ms = col_double(),
## .. energy = col_double(),
## .. instrumentalness = col_double(),
## .. key = col_character(),
## .. liveness = col_double(),
## .. loudness = col_double(),
## .. mode = col_character(),
## .. speechiness = col_double(),
## .. tempo = col_double(),
## .. time_signature = col_character(),
## .. valence = col_double()
## .. )
## - attr(*, "problems")=<externalptr>
columns <- colnames(tracks)
columns
## [1] "genre" "artist_name" "track_name" "track_id"
## [5] "popularity" "acousticness" "danceability" "duration_ms"
## [9] "energy" "instrumentalness" "key" "liveness"
## [13] "loudness" "mode" "speechiness" "tempo"
## [17] "time_signature" "valence" "isKey1"
numeric_columns <- unlist(lapply(tracks, is.numeric))
numeric_columns
## genre artist_name track_name track_id
## FALSE FALSE FALSE FALSE
## popularity acousticness danceability duration_ms
## TRUE TRUE TRUE TRUE
## energy instrumentalness key liveness
## TRUE TRUE TRUE TRUE
## loudness mode speechiness tempo
## TRUE TRUE TRUE TRUE
## time_signature valence isKey1
## FALSE TRUE TRUE
numeric_spotifydf <- tracks[,numeric_columns] %>% select (-c(isKey1))
colnames(numeric_spotifydf)
## [1] "popularity" "acousticness" "danceability" "duration_ms"
## [5] "energy" "instrumentalness" "key" "liveness"
## [9] "loudness" "mode" "speechiness" "tempo"
## [13] "valence"
Correlation based on feature groups
Use Corrplot and stats library to plot correlation based on feature groups, numeric plots.
Found this library more helpful to group into clusters for higher or similar correlation between features.
corr_df2 <- stats::cor(numeric_spotifydf)
col3 = hcl.colors(10, "YlOrRd", rev = TRUE)
corr1 <- corrplot(corr_df2, col=col3, method = 'number')
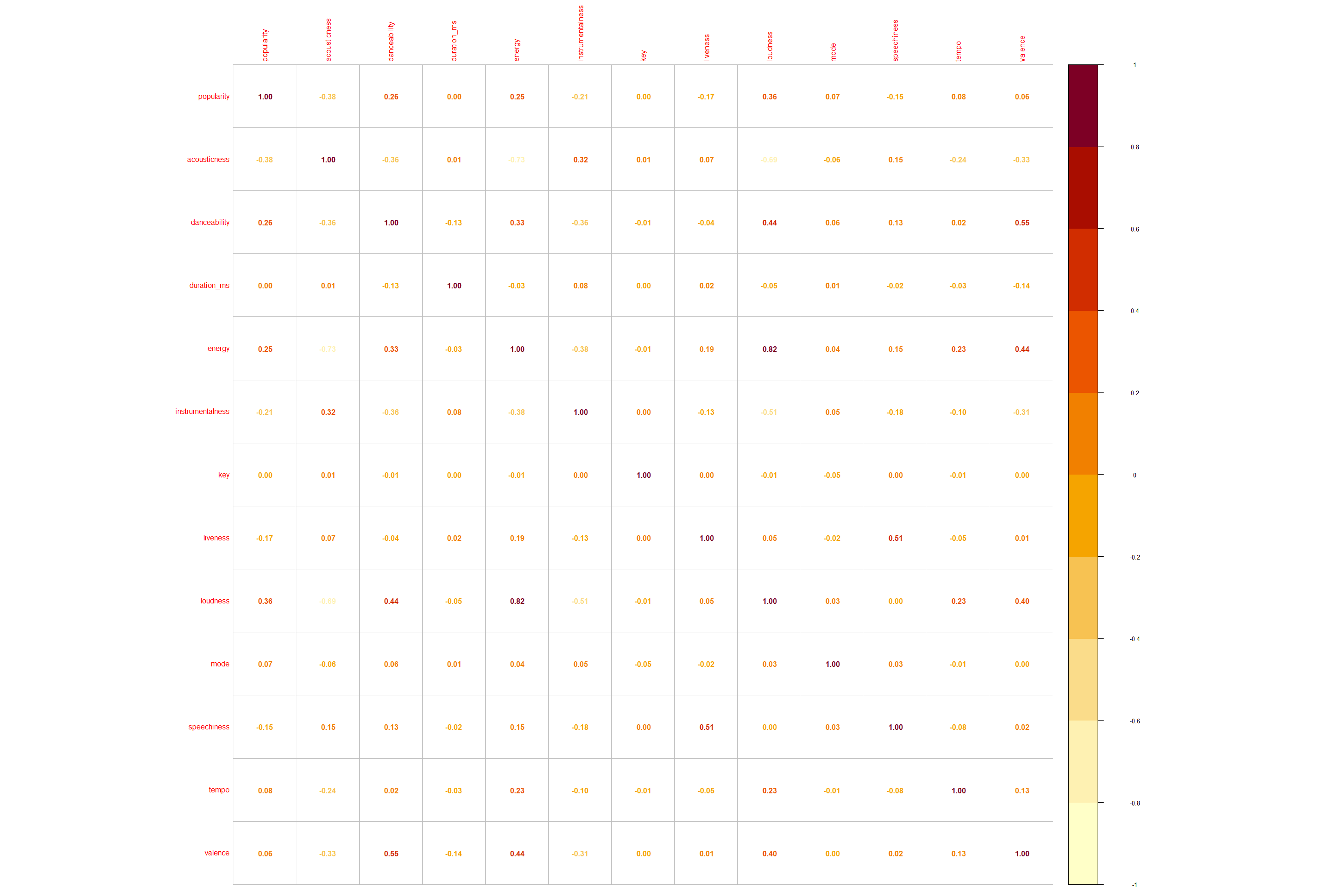
There is a high correlation between energy and loudness features and similarly there is a second highest correlation between valence and danceability where valence is positiveness or negativeness of a track defined by (cheerful vs sad, depressive tune, lyrics)
Spotify tracks by Genre in the US
For each feature, plot grouping w.r.t Popularity.
genres_df <- tracks %>%
select(popularity, genre)%>%
count(popularity, genre)
by_genres <- tracks %>% group_by(genre, popularity)
by_genres %>% summarise(
popularity = mean(popularity),
)
## `summarise()` has grouped output by 'genre'. You can override using the `.groups` argument.
## # A tibble: 1,802 x 2
## # Groups: genre [26]
## genre popularity
## <fct> <dbl>
## 1 A Capella 0
## 2 A Capella 1
## 3 A Capella 2
## 4 A Capella 3
## 5 A Capella 4
## 6 A Capella 5
## 7 A Capella 6
## 8 A Capella 7
## 9 A Capella 8
## 10 A Capella 9
## # ... with 1,792 more rows
by_genre <- by_genres %>% summarise(n = n())
## `summarise()` has grouped output by 'genre'. You can override using the `.groups` argument.
by_genre %>% summarise(n = sum(n)) %>% filter(n>0)
## # A tibble: 26 x 2
## genre n
## <fct> <int>
## 1 A Capella 119
## 2 Alternative 9263
## 3 Anime 8936
## 4 Blues 9023
## 5 Childrens Music 14756
## 6 Classical 9256
## 7 Comedy 9681
## 8 Country 8664
## 9 Dance 8701
## 10 Electronic 9377
## # ... with 16 more rows
#vtree(genres_df, "genre")
colnames(by_genre)
## [1] "genre" "popularity" "n"
ggplot(genres_df)+
geom_point(aes(x = genre, y= n))
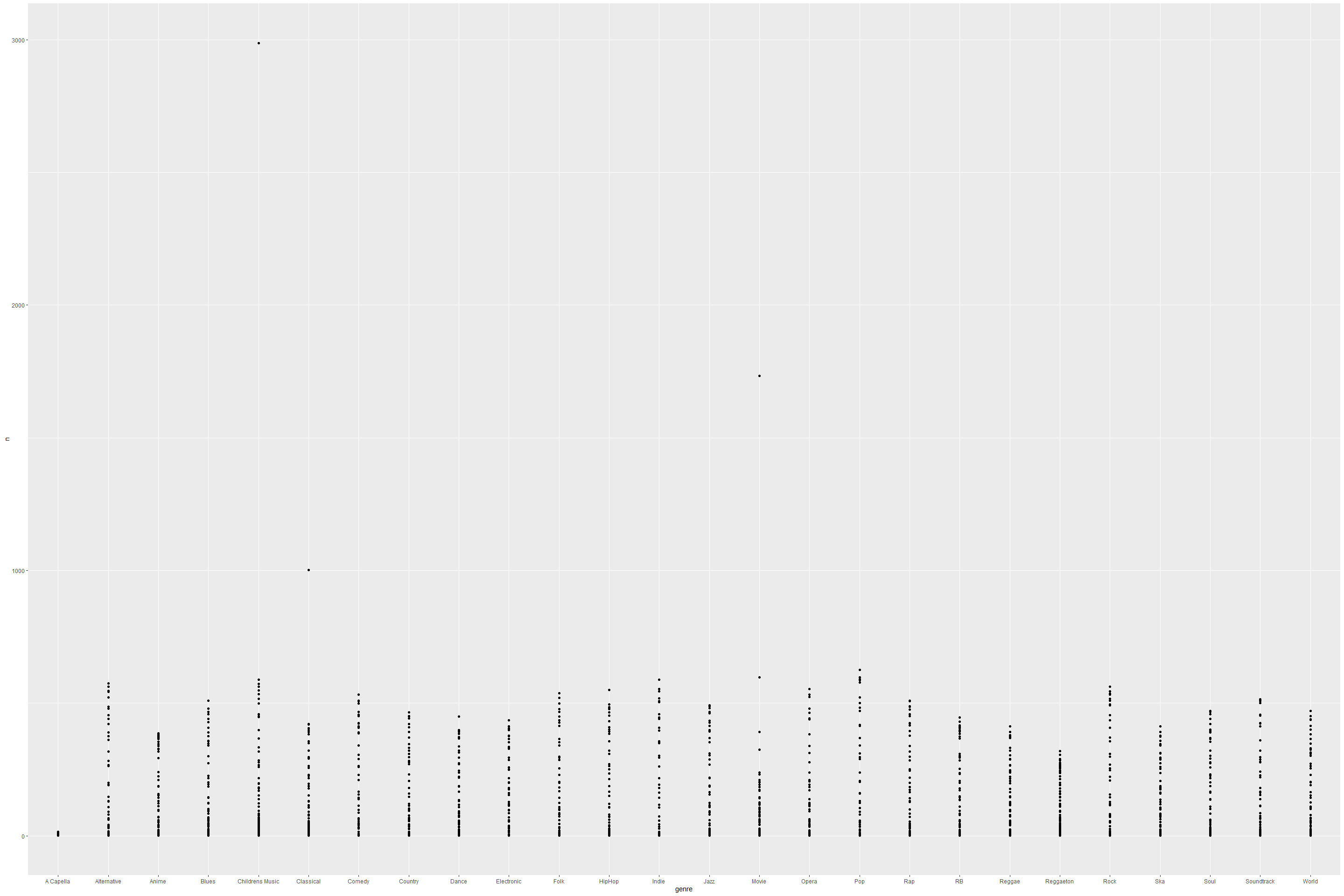
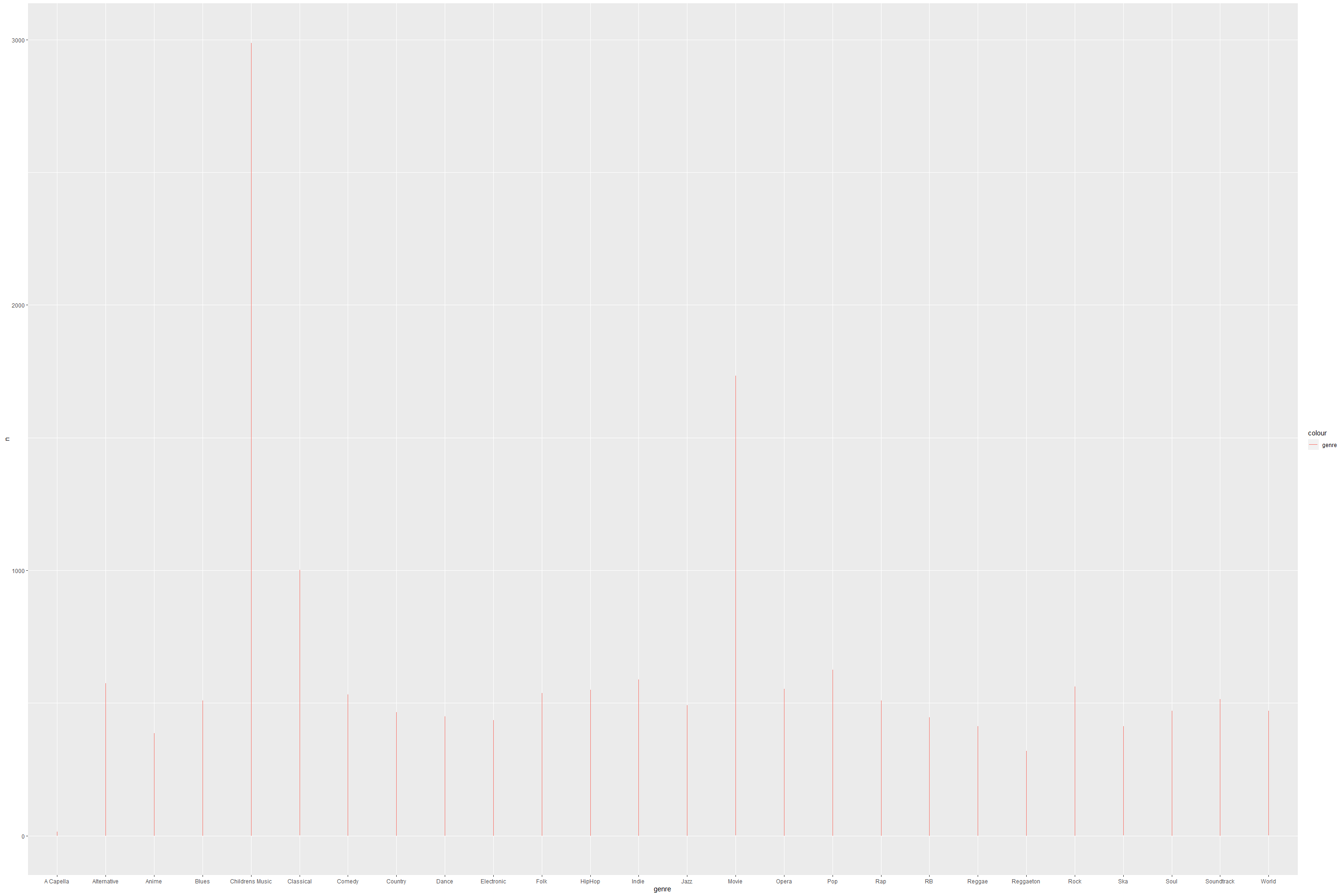
genres_df %>% ggplot(aes(x = genre, y= n))+
geom_line(aes(color = "genre"))
ggplot(data=by_genre,aes(x = genre, y = n, fill=genre)) +
geom_bar(stat="identity", width=0.5, position=position_dodge())+
coord_flip()+
labs(title = "Spotify tracks by Genre in US", y= NULL)
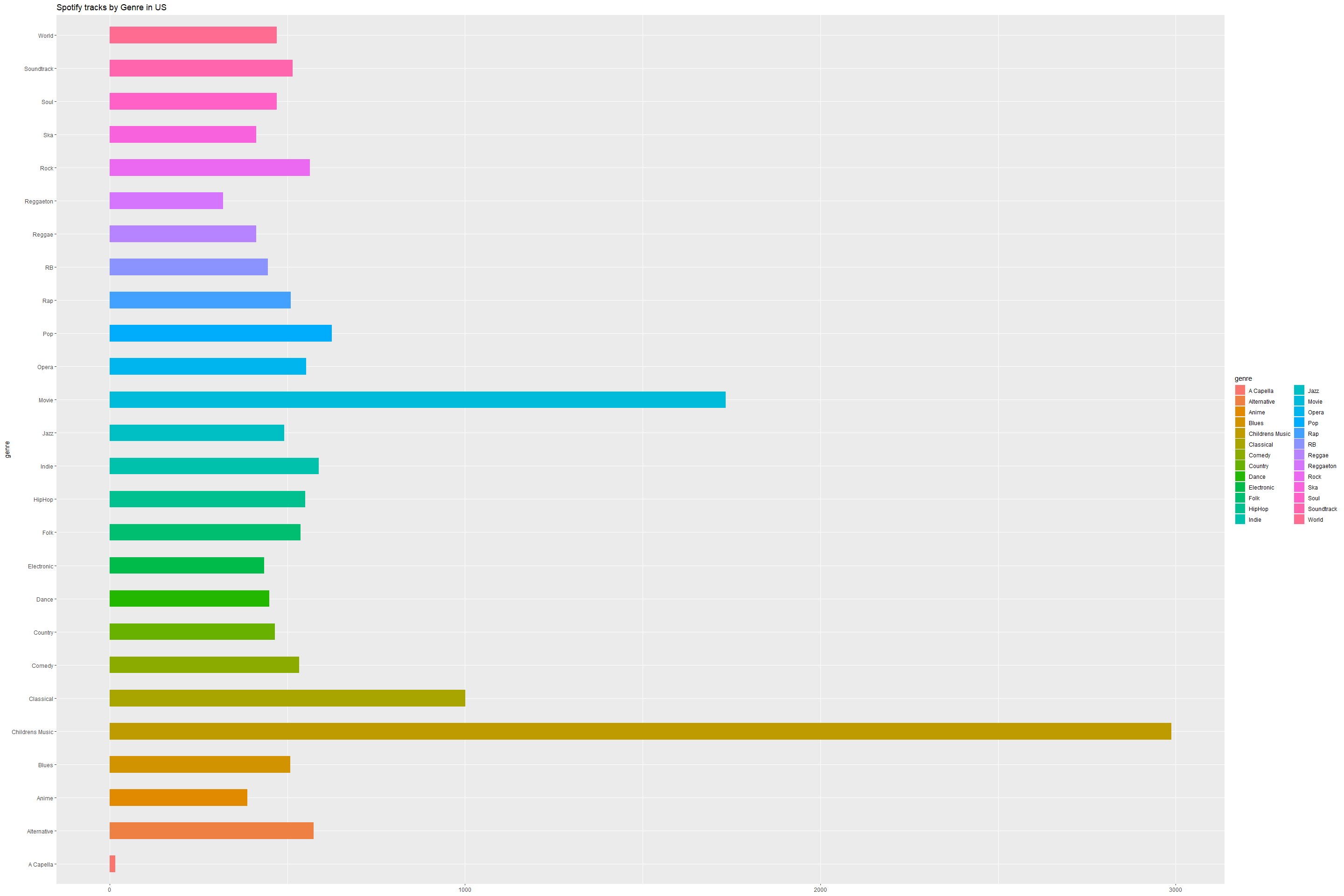
Group by Genres and select all features except text based features.
genres_df <- tracks %>%
select(-c(artist_name, track_name, track_id, time_signature, key))
Data summary and density distribution for all spotify features
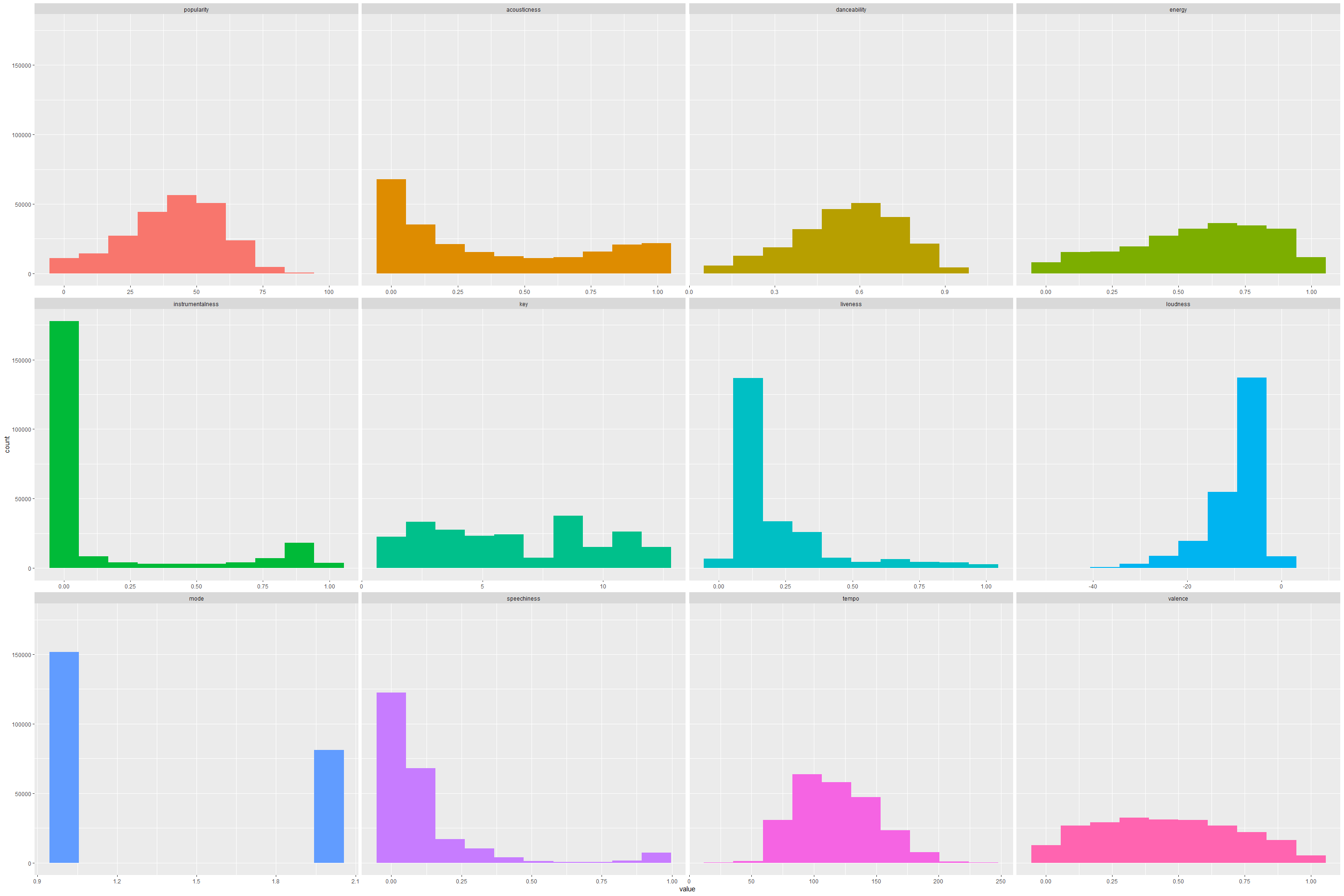
Each of features do seem to have different types of density, suggesting distributions are different from each other. It would have been nice if some normalization technique or re-sampling of features was done. But in the interest of time, we could not do this. From the above density plots, it would be reasonable to find some kind of normalization between feature data.
spotify_summary <- datasummary_skim(numeric_spotifydf)
spotify_summary
| Unique (\#) | Missing (%) | Mean | SD | Min | Median | Max | ||
|---|---|---|---|---|---|---|---|---|
| popularity | 101 | 0 | 41.1 | 18.2 | 0.0 | 43.0 | 100.0 | |
| acousticness | 4734 | 0 | 0.4 | 0.4 | 0.0 | 0.2 | 1.0 | |
| danceability | 1295 | 0 | 0.6 | 0.2 | 0.1 | 0.6 | 1.0 | |
| duration\_ms | 70749 | 0 | 235122.3 | 118935.9 | 15387.0 | 220427.0 | 5552917.0 | |
| energy | 2517 | 0 | 0.6 | 0.3 | 0.0 | 0.6 | 1.0 | |
| instrumentalness | 5400 | 0 | 0.1 | 0.3 | 0.0 | 0.0 | 1.0 | |
| key | 12 | 0 | 6.3 | 3.5 | 1.0 | 6.0 | 12.0 | |
| liveness | 1732 | 0 | 0.2 | 0.2 | 0.0 | 0.1 | 1.0 | |
| loudness | 27923 | 0 | -9.6 | 6.0 | -52.5 | -7.8 | 3.7 | |
| mode | 2 | 0 | 1.3 | 0.5 | 1.0 | 1.0 | 2.0 | |
| speechiness | 1641 | 0 | 0.1 | 0.2 | 0.0 | 0.1 | 1.0 | |
| tempo | 78512 | 0 | 117.7 | 30.9 | 30.4 | 115.8 | 242.9 | |
| valence | 1692 | 0 | 0.5 | 0.3 | 0.0 | 0.4 | 1.0 |
Plot the density distributions of each of features.
spotify_histograms <- numeric_spotifydf[,-c(4)]
plot_num(spotify_histograms)
## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.
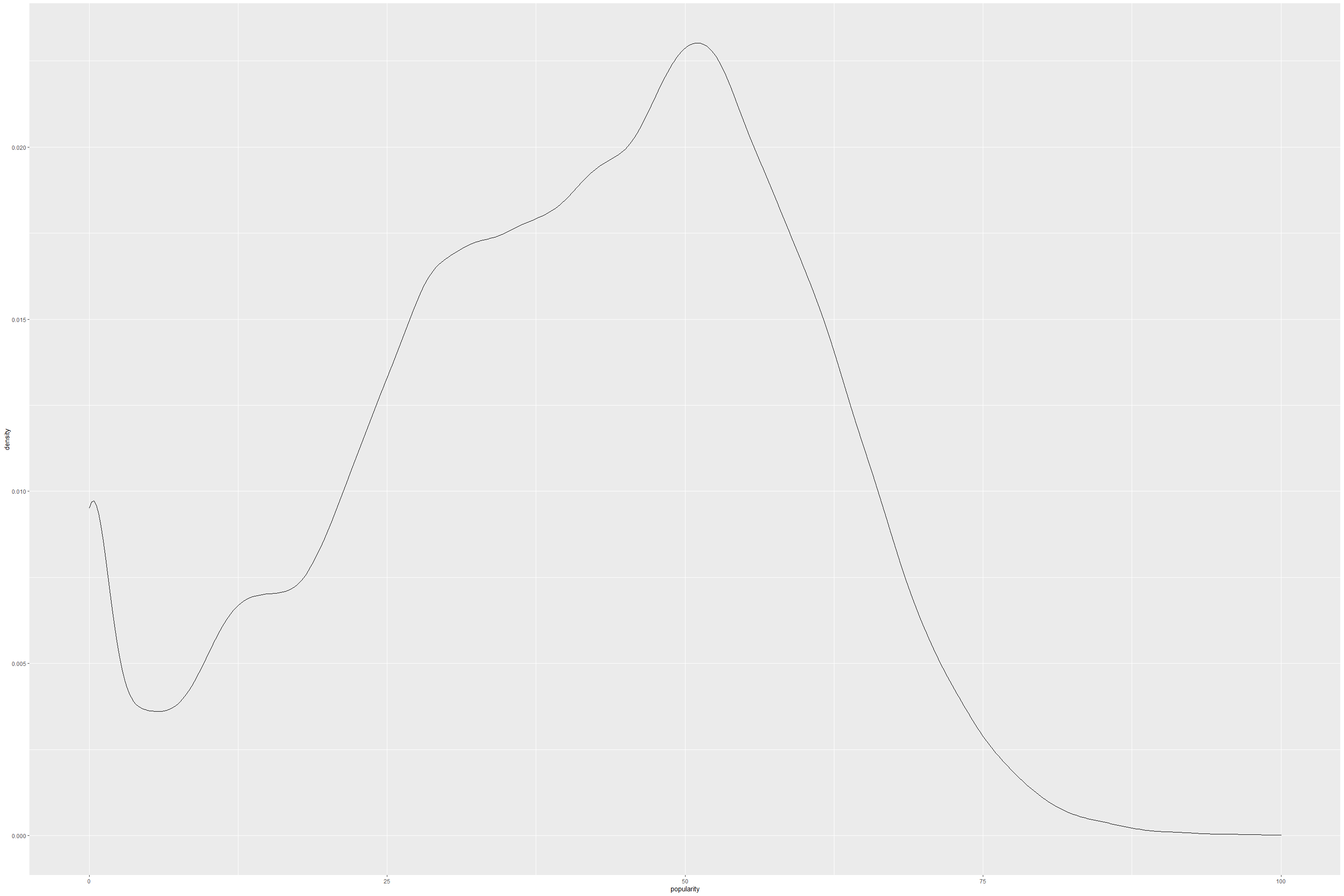
ggplot(tracks, aes(popularity)) +
geom_density()
ggplot(tracks, aes(energy)) +
geom_density()
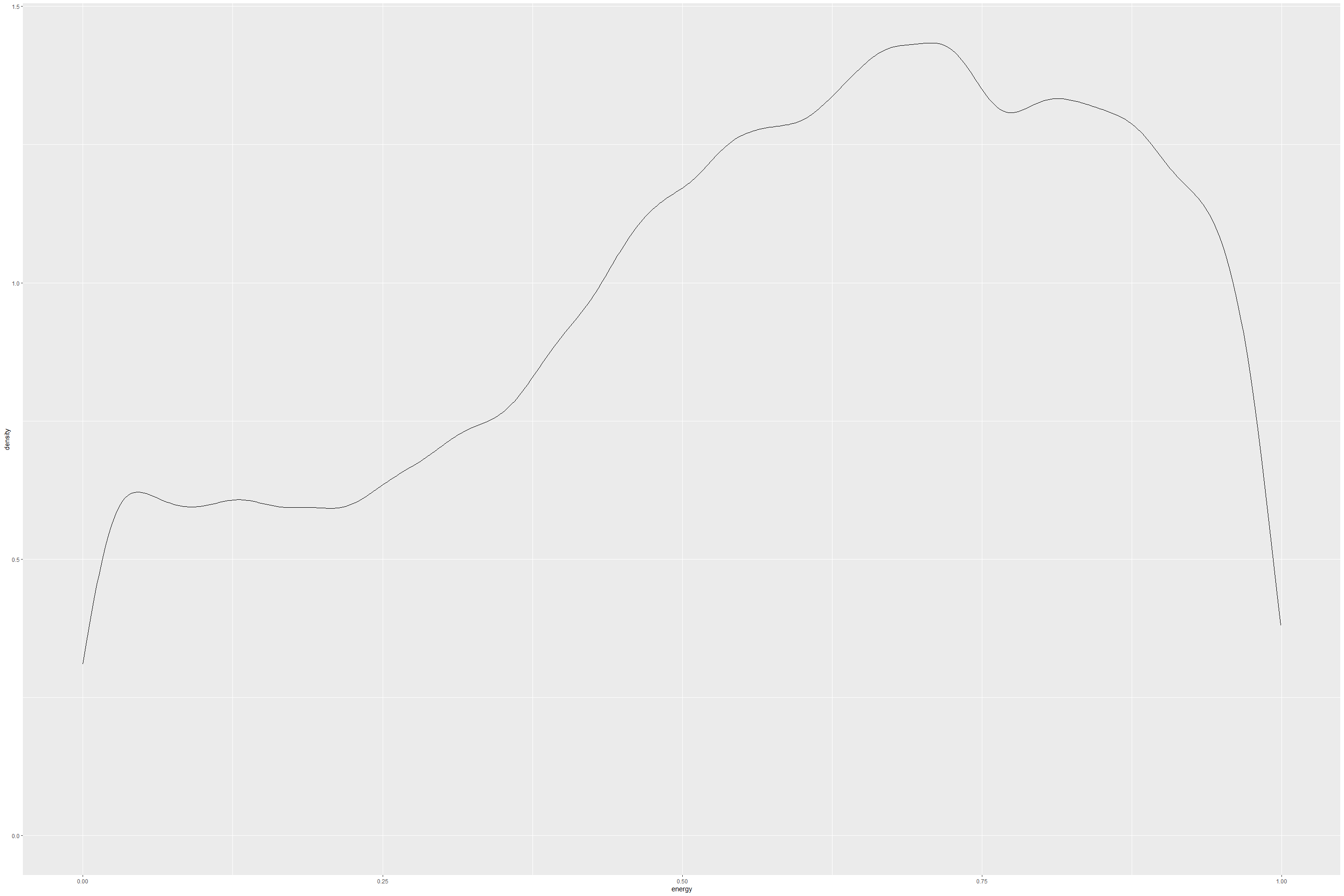
ggplot(tracks, aes(danceability)) +
geom_density()

ggplot(tracks, aes(key)) +
geom_density()
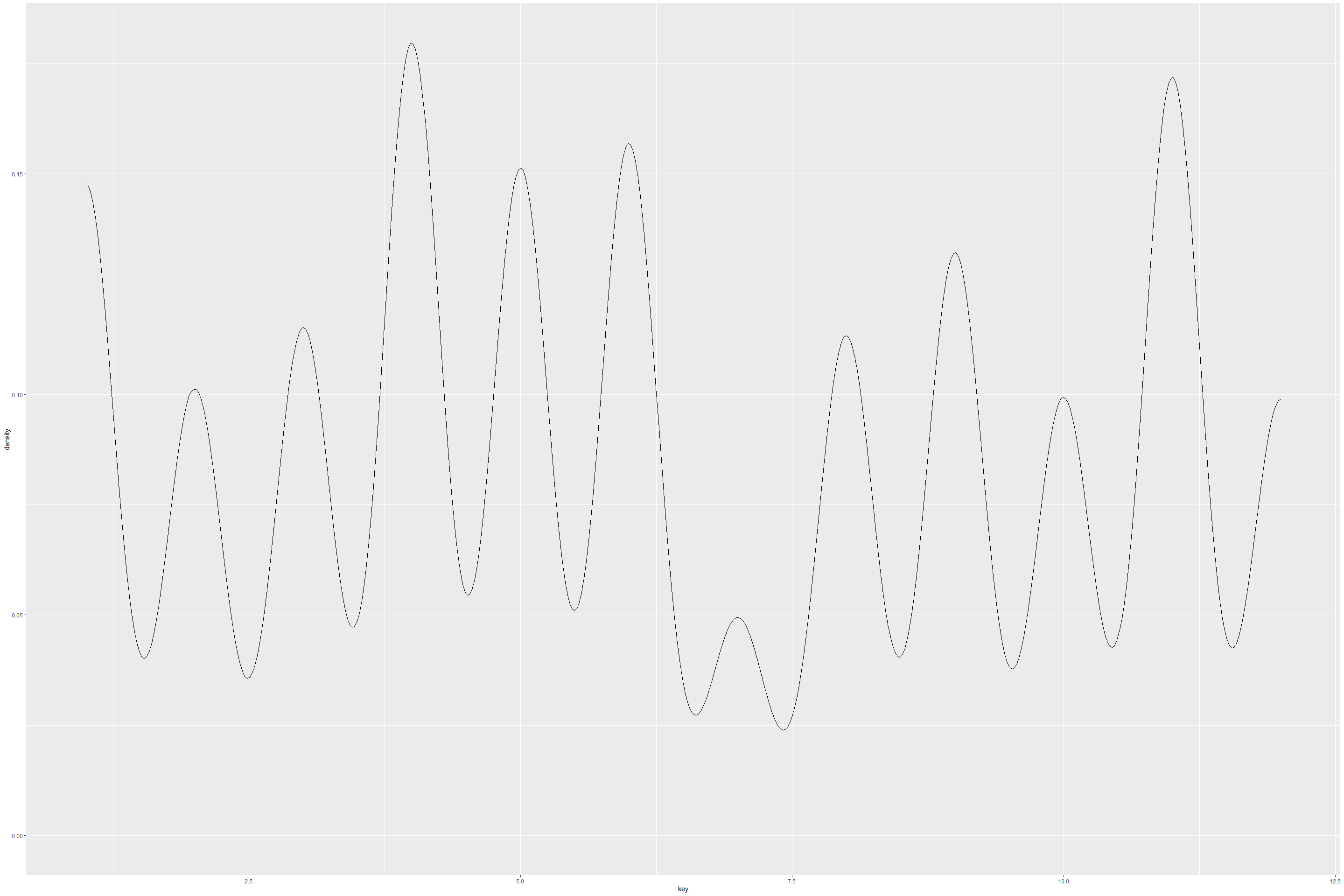
Linear Regression Modelling to check the linear fit
Check linear fit between all features vs popularity
This is multiple regression since we have multiple predictors vs one
response variable.
We find a linear fit for y = [popularity] and X = [ acousticness, danceability, duration_ms, energy, instrumentalness, liveness, loudness, speechiness, tempo, valence] to check model fit.
lmfit = lm(popularity ~ acousticness + danceability + duration_ms +energy + instrumentalness + liveness + loudness + speechiness + tempo + valence, numeric_spotifydf )
summary(lmfit)
##
## Call:
## lm(formula = popularity ~ acousticness + danceability + duration_ms +
## energy + instrumentalness + liveness + loudness + speechiness +
## tempo + valence, data = numeric_spotifydf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -58.034 -10.215 1.413 11.058 57.368
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 55.3882318323 0.3440857483 160.972 < 0.0000000000000002 ***
## acousticness -11.9348863471 0.1547306909 -77.133 < 0.0000000000000002 ***
## danceability 17.7399712075 0.2421276181 73.267 < 0.0000000000000002 ***
## duration_ms 0.0000024569 0.0000002816 8.726 < 0.0000000000000002 ***
## energy -5.6278359232 0.2794090244 -20.142 < 0.0000000000000002 ***
## instrumentalness -4.3105903938 0.1330431074 -32.400 < 0.0000000000000002 ***
## liveness -9.6705519516 0.2011430478 -48.078 < 0.0000000000000002 ***
## loudness 0.7150992187 0.0112616140 63.499 < 0.0000000000000002 ***
## speechiness -8.1081609287 0.2298549766 -35.275 < 0.0000000000000002 ***
## tempo -0.0042749795 0.0011180789 -3.824 0.000132 ***
## valence -13.2258861142 0.1659321212 -79.707 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.92 on 232714 degrees of freedom
## Multiple R-squared: 0.2339, Adjusted R-squared: 0.2339
## F-statistic: 7106 on 10 and 232714 DF, p-value: < 0.00000000000000022
plot(lmfit)
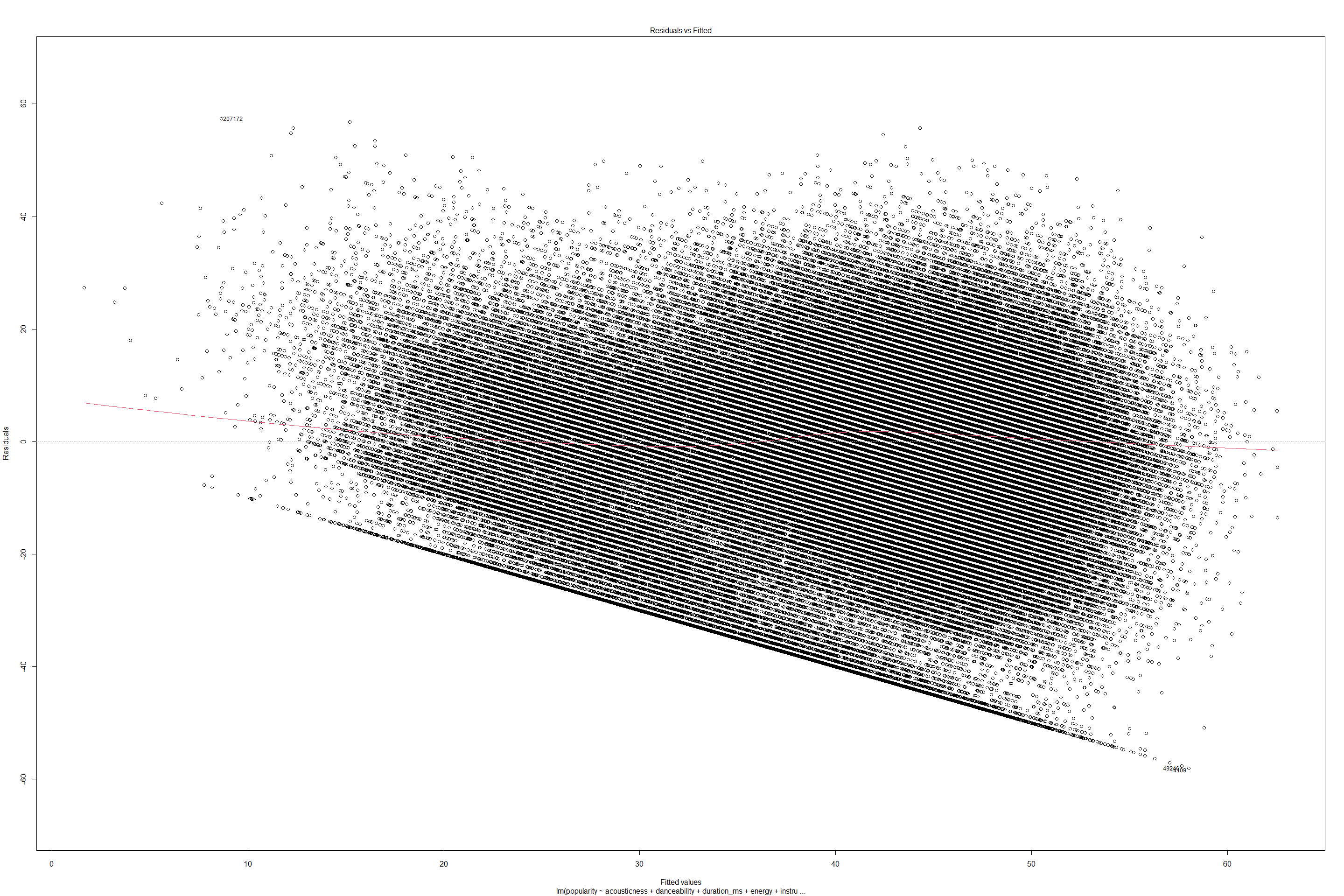
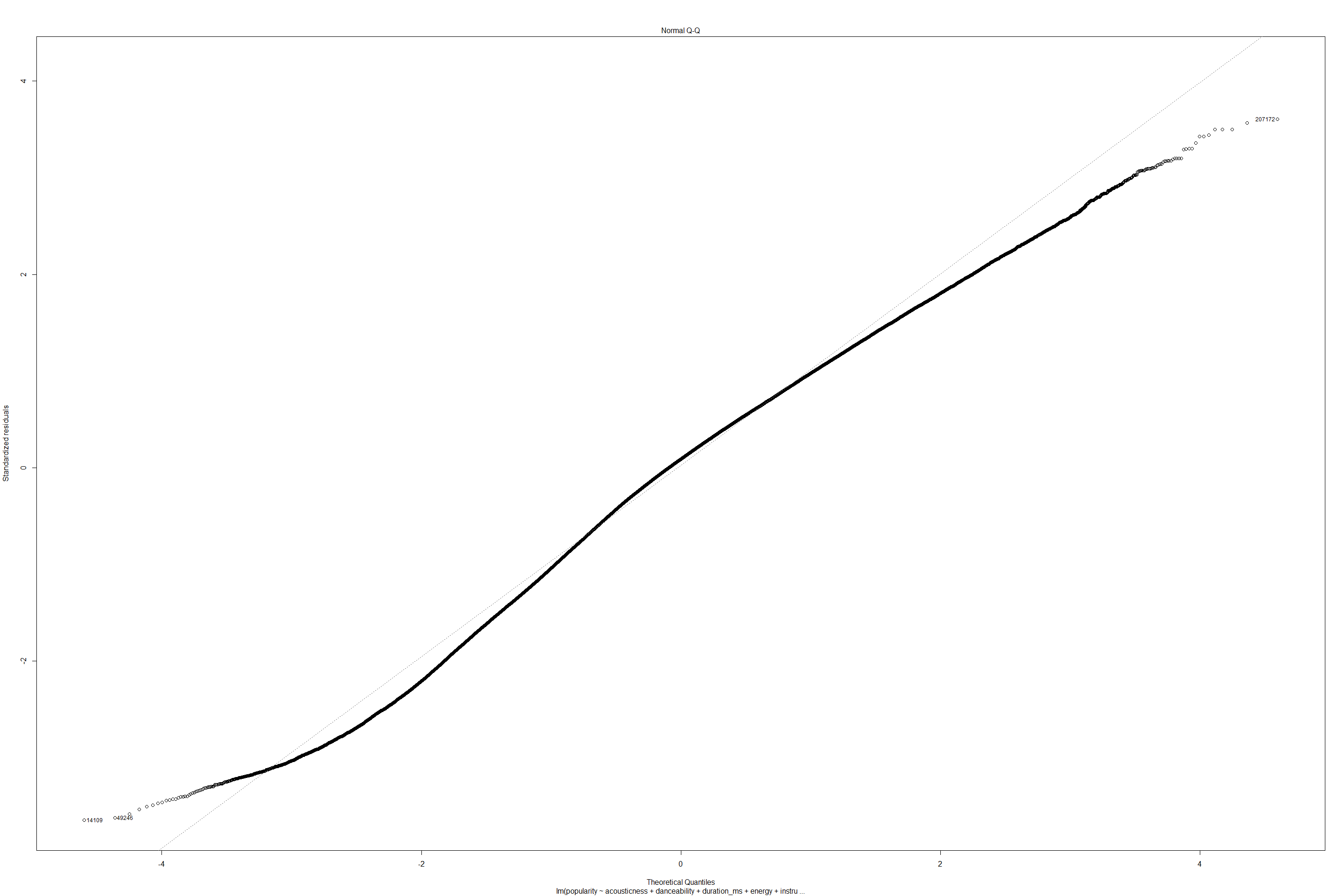


The summary of linear fit suggests that R-squared value is 0.2339 which is not significant enough to explain how much percentage of data fits linearly. Standard error is 15.92 suggests this is 15.92 standard deviations of the residuals away from true regression fit. The p-value of less than 0.01 suggests that null hypothesis that predictors and response variables are not related can be rejected. Hence observed values of response variable are no better than predicted values, by a chance. However since this is a multiple linear regression, F-statistic may also be relevant here since it checks if atleast one of the predictors’ coefficients is non-zero. F-statistic = (SSR/SSE) = (Sum of squares regression) / (sum of squares error) -> is the ratio of variance explained / variance that cannot be explained. The standard errors suggest that about ~75% of variance in data cannot be explained. P(> |t|) for each of features also suggests null hypothesis that there is no relation between predictors and response variable - must be rejected.
checking coefficients
coefficients(lmfit)
## (Intercept) acousticness danceability duration_ms
## 55.388231832270 -11.934886347087 17.739971207543 0.000002456887
## energy instrumentalness liveness loudness
## -5.627835923246 -4.310590393787 -9.670551951580 0.715099218724
## speechiness tempo valence
## -8.108160928731 -0.004274979477 -13.225886114236
lmfit2 = lm(popularity ~ acousticness + danceability +energy + instrumentalness + liveness + loudness + speechiness + tempo + valence + key+mode+(energy * loudness) + (valence * danceability) , numeric_spotifydf )
summary(lmfit2)
##
## Call:
## lm(formula = popularity ~ acousticness + danceability + energy +
## instrumentalness + liveness + loudness + speechiness + tempo +
## valence + key + mode + (energy * loudness) + (valence * danceability),
## data = numeric_spotifydf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -60.60 -10.16 1.42 10.98 57.75
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 48.642916 0.383028 126.996 < 0.0000000000000002 ***
## acousticness -11.869822 0.154208 -76.973 < 0.0000000000000002 ***
## danceability 26.491613 0.379808 69.750 < 0.0000000000000002 ***
## energy -4.806738 0.303869 -15.818 < 0.0000000000000002 ***
## instrumentalness -4.074058 0.133798 -30.449 < 0.0000000000000002 ***
## liveness -9.667267 0.201558 -47.963 < 0.0000000000000002 ***
## loudness 0.627526 0.012114 51.802 < 0.0000000000000002 ***
## speechiness -8.102821 0.232924 -34.787 < 0.0000000000000002 ***
## tempo -0.008507 0.001124 -7.569 0.0000000000000376 ***
## valence 0.836879 0.480117 1.743 0.0813 .
## key 0.038810 0.009514 4.079 0.0000452207135986 ***
## mode 1.895830 0.069785 27.167 < 0.0000000000000002 ***
## energy:loudness 0.269525 0.024068 11.198 < 0.0000000000000002 ***
## danceability:valence -23.230354 0.749642 -30.989 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.87 on 232711 degrees of freedom
## Multiple R-squared: 0.2393, Adjusted R-squared: 0.2392
## F-statistic: 5630 on 13 and 232711 DF, p-value: < 0.00000000000000022
The summary of linear fit suggests that R-squared value is 0.2392 which should be significant enough to explain how much percentage of data fits linearly. Standard error is 15.92 suggests this is 15.92 standard deviations of the residuals away from true regression fit. The p-value of less than 0.01 suggests that null hypothesis that predictors and response variables are not related can be rejected. Hence observed values of response variable are no better than predicted values, by a chance. However since this is a multiple linear regression, F-statistic may also be relevant here since it checks if atleast one of the predictors’ coefficients is non-zero. F-statistic = (SSR/SSE) = (Sum of squares regression) / (sum of squares error) -> is the ratio of variance explained / varinace that cannot be explained. The standard errors suggest that about ~75% of variance in data cannot be explained. P(> |t|) for each of features also suggests null hypothesis that there is no relation between predictors and response variable - must be rejected. From p(>|t|) = 0.08 for valence, seems to indicate null hypothesis true for valence and popularity score suggesting that valence has no influence on popularity score.
anova(lmfit2)
## Analysis of Variance Table
##
## Response: popularity
## Df Sum Sq Mean Sq F value Pr(>F)
## acousticness 1 11195075 11195075 44473.7751 < 0.00000000000000022
## danceability 1 1227403 1227403 4876.0073 < 0.00000000000000022
## energy 1 213263 213263 847.2141 < 0.00000000000000022
## instrumentalness 1 433266 433266 1721.1992 < 0.00000000000000022
## liveness 1 1482439 1482439 5889.1653 < 0.00000000000000022
## loudness 1 1638613 1638613 6509.5846 < 0.00000000000000022
## speechiness 1 121368 121368 482.1469 < 0.00000000000000022
## tempo 1 29421 29421 116.8794 < 0.00000000000000022
## valence 1 1653514 1653514 6568.7823 < 0.00000000000000022
## key 1 1943 1943 7.7177 0.005469
## mode 1 172847 172847 686.6535 < 0.00000000000000022
## energy:loudness 1 12763 12763 50.7023 0.000000000001078
## danceability:valence 1 241728 241728 960.2924 < 0.00000000000000022
## Residuals 232711 58578725 252
##
## acousticness ***
## danceability ***
## energy ***
## instrumentalness ***
## liveness ***
## loudness ***
## speechiness ***
## tempo ***
## valence ***
## key **
## mode ***
## energy:loudness ***
## danceability:valence ***
## Residuals
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
plot(lmfit2)
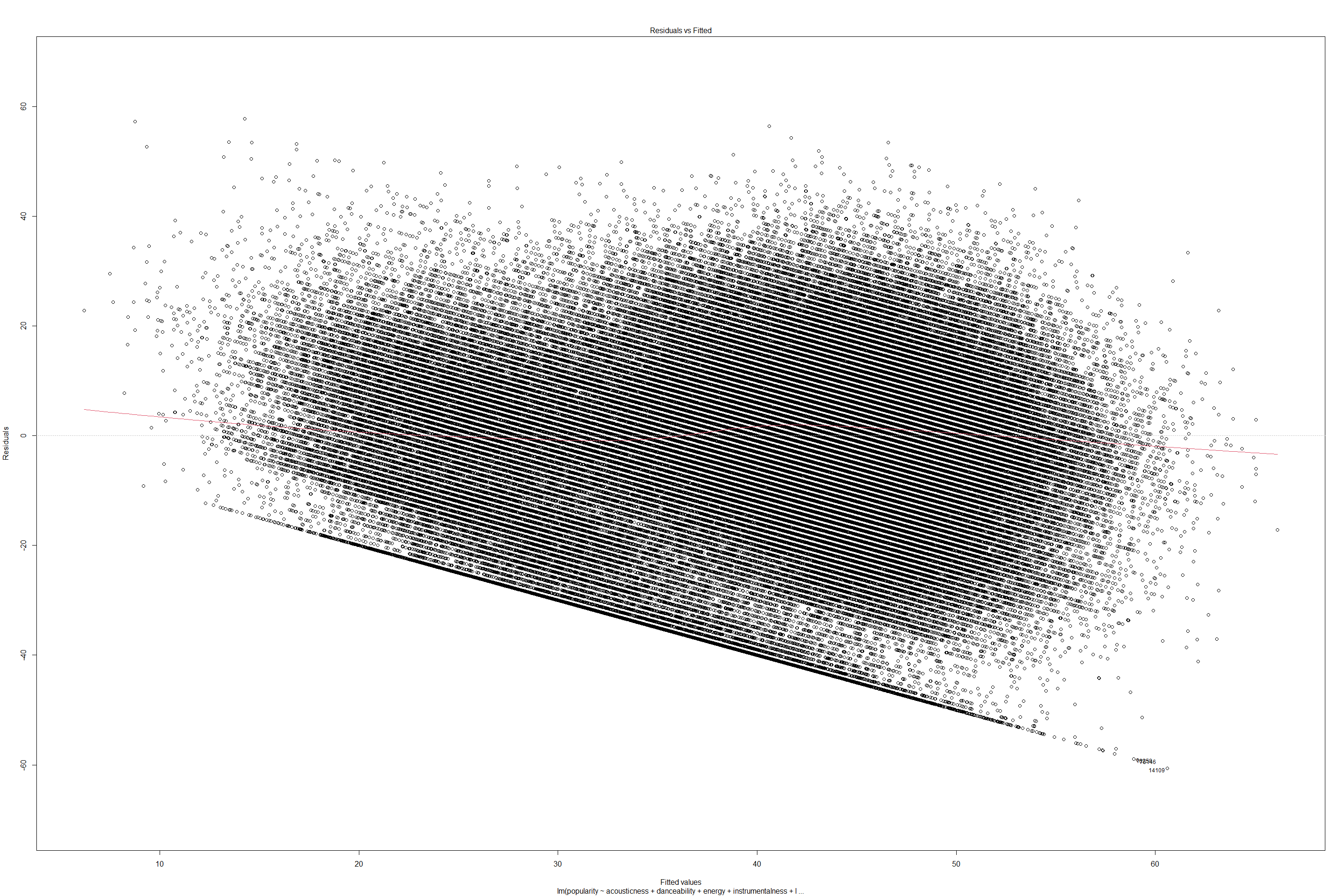
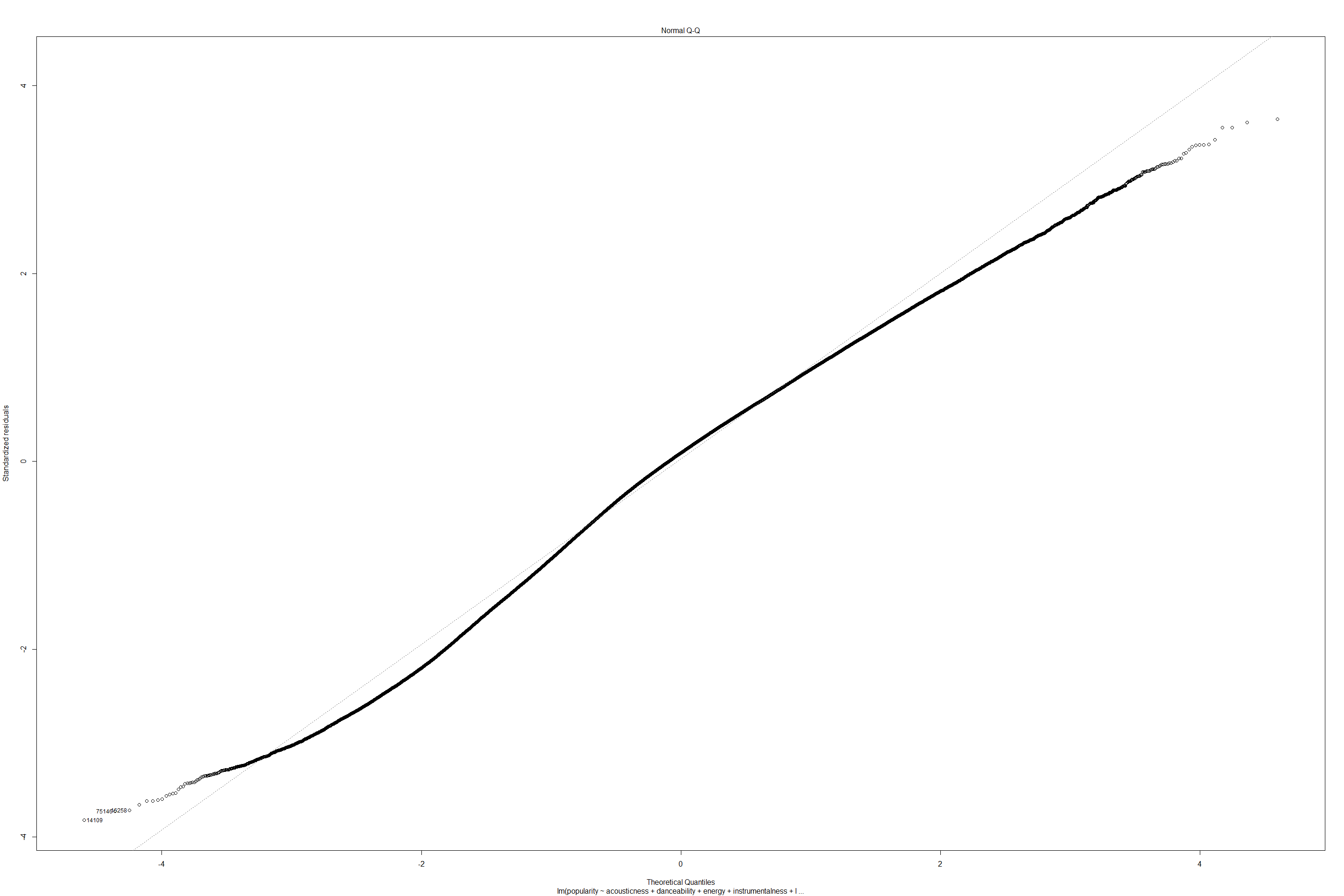

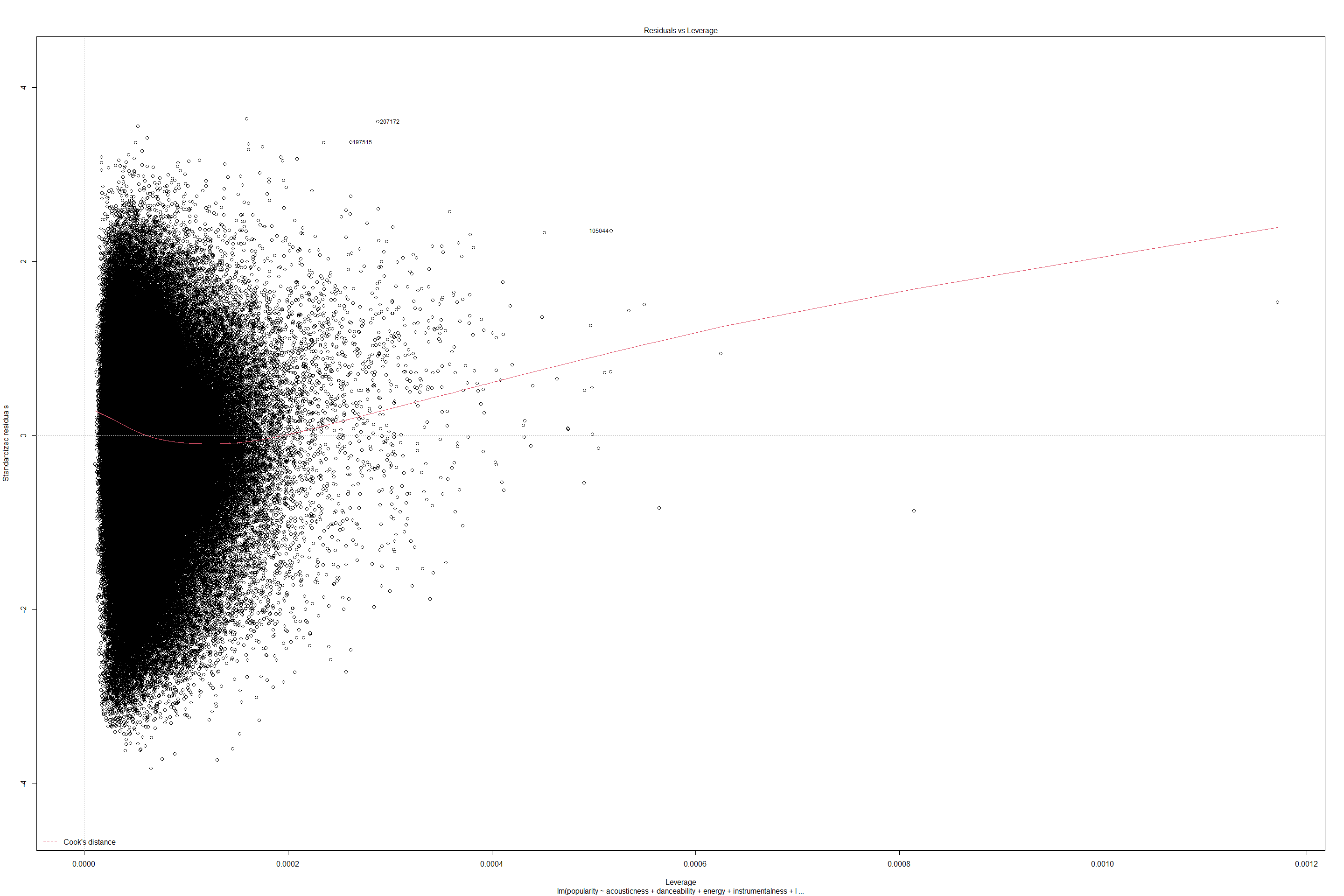
get model summary for Linear regression and Generalized Linear regression with Gaussian.
models <- list(
"OLS" = lmfit2,
"GLM" = glm(popularity ~ acousticness + danceability +energy + instrumentalness + liveness + loudness + speechiness + tempo + valence + key+mode+(energy * loudness) + (valence * danceability) , data = numeric_spotifydf , family = gaussian)
)
modelsummary(models,
fmt = 1,
estimate = c(
"{estimate} ({std.error})",
"{estimate} [{conf.low}, {conf.high}]"),
statistic = NULL,
coef_omit = "Intercept",
output = "table1.png")
## save_kable will have the best result with magick installed.
Get standard errors, statistics and p-values for each of models.
modelsummary(models,gof_omit = ".*",
statistic = c("conf.int",
"s.e. = {std.error}",
"t = {statistic}",
"p = {p.value}"),
output = "table2.png")
## save_kable will have the best result with magick installed.
taking linear regression fit analysis further, using model summary package we are able to compare how features fit in comparison between linear regression as well as Gaussian Generalized Linear regression fit. There is no change in P-values or null hypothesis analysis. However, individual feature’s standard errors seems significant and are very low. This suggests that linear regression (generalized or OLS) seem to be overfitted.
Random Forest Regression Fit
Random Forest Regression fit by train and test split.
Create train and test sets
train = sample(1:nrow(numeric_spotifydf), 300)
rf.spotify = randomForest(popularity~., data = numeric_spotifydf, subset = train)
rf.spotify
##
## Call:
## randomForest(formula = popularity ~ ., data = numeric_spotifydf, subset = train)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 4
##
## Mean of squared residuals: 256.521
## % Var explained: 28.69
In case of Random Forest regression, number of trees are 500 with 4
variables at each split. as well the MSR is 252.81 and explained
variance is still low 24.79 % of variance explained.
The following plot suggests that 50 trees or so is enough to fit the
model with RFR.
plot(rf.spotify)
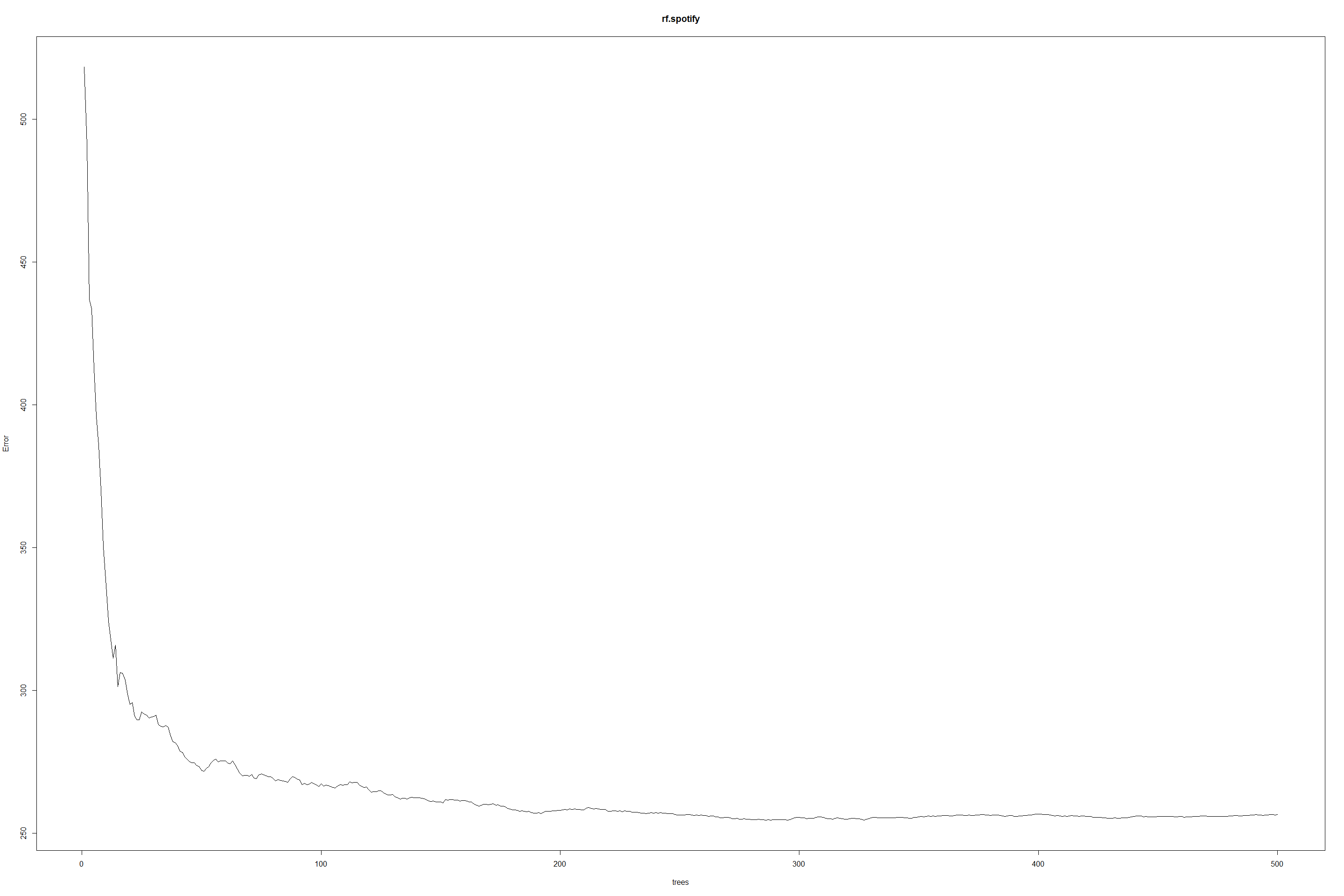
For each variables 1 to 17 of features, find Out-of-bag and test errors for each fit.
oob.err = double(17)
test.err = double(17)
for(mtry in 1:17){
fit = randomForest(popularity~., data = numeric_spotifydf, subset=train, mtry=mtry, ntree = 350)
oob.err[mtry] = fit$mse[350]
pred = predict(fit, numeric_spotifydf[-train,])
test.err[mtry] = with(numeric_spotifydf[-train,], mean( (popularity-pred)^2 ))
}
## Warning in randomForest.default(m, y, ...): invalid mtry: reset to within valid
## range
## Warning in randomForest.default(m, y, ...): invalid mtry: reset to within valid
## range
## Warning in randomForest.default(m, y, ...): invalid mtry: reset to within valid
## range
## Warning in randomForest.default(m, y, ...): invalid mtry: reset to within valid
## range
## Warning in randomForest.default(m, y, ...): invalid mtry: reset to within valid
## range
Random Forest Regression Trees 17*350 trees with MSE for OOB and Test errors
matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error", lwd=6)
legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))
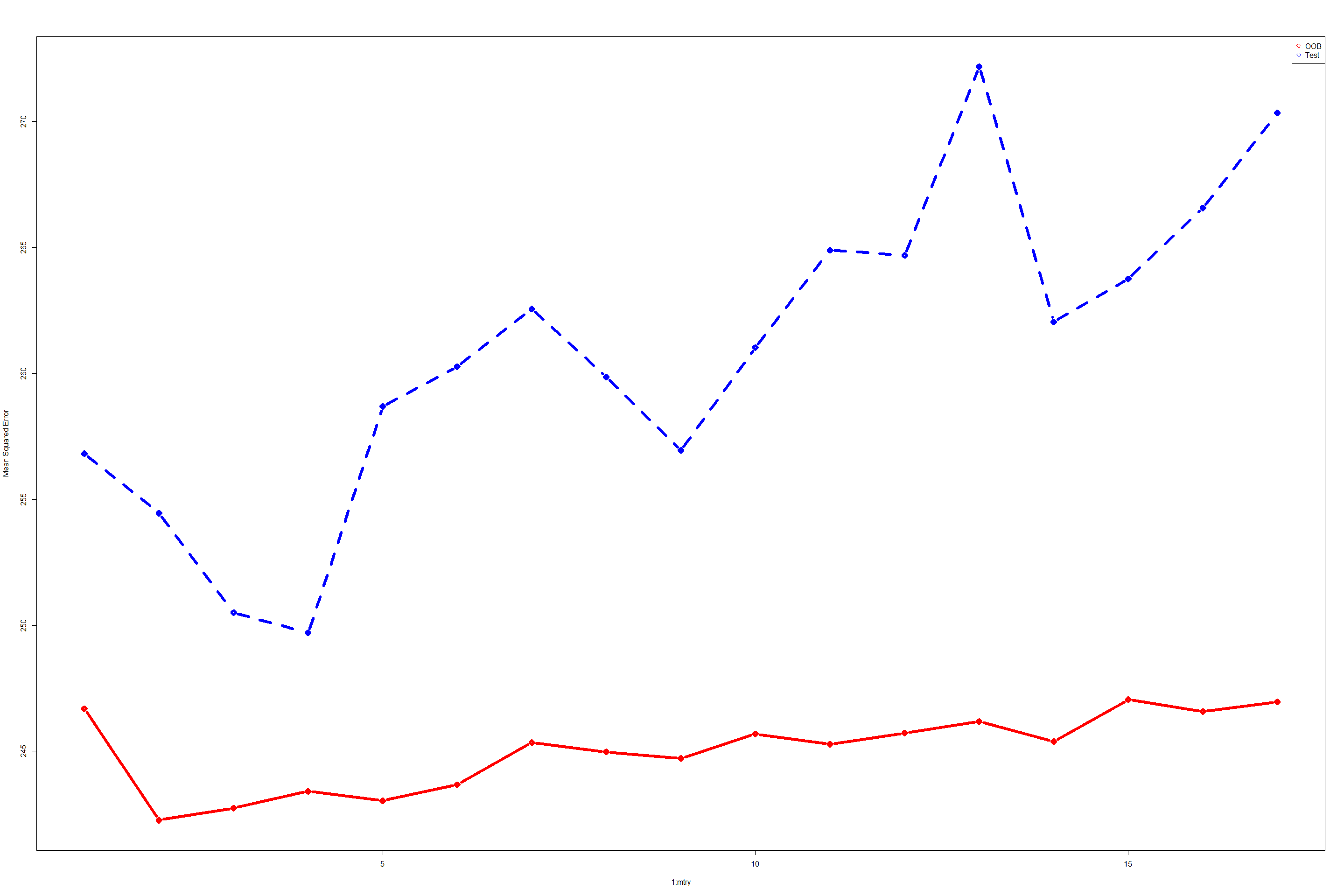
The above plot suggests that Out-Of-Bag error estimates (red colored curve) is very far apart from test error estimates. There is no correlation between OOB and test errors. Errors never really tends to minimize as the number of features increase during training.
oob.err
## [1] 256.8133 254.4565 250.5019 249.7019 258.6919 260.2703 262.5641 259.8550
## [9] 256.9463 261.0295 264.8954 264.6887 272.1771 262.0539 263.7588 266.5758
## [17] 270.3555
test.err
## [1] 246.6887 242.2641 242.7439 243.4092 243.0337 243.6699 245.3455 244.9732
## [9] 244.7181 245.6833 245.2837 245.7247 246.1798 245.3829 247.0487 246.5748
## [17] 246.9585
Basic Random Forest on all features
rf.spotify1 = randomForest(popularity~., data = numeric_spotifydf, subset = train, importance = TRUE)
rf.spotify1
##
## Call:
## randomForest(formula = popularity ~ ., data = numeric_spotifydf, importance = TRUE, subset = train)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 4
##
## Mean of squared residuals: 252.5125
## % Var explained: 29.8
summary(rf.spotify1)
## Length Class Mode
## call 5 -none- call
## type 1 -none- character
## predicted 300 -none- numeric
## mse 500 -none- numeric
## rsq 500 -none- numeric
## oob.times 300 -none- numeric
## importance 24 -none- numeric
## importanceSD 12 -none- numeric
## localImportance 0 -none- NULL
## proximity 0 -none- NULL
## ntree 1 -none- numeric
## mtry 1 -none- numeric
## forest 11 -none- list
## coefs 0 -none- NULL
## y 300 -none- numeric
## test 0 -none- NULL
## inbag 0 -none- NULL
## terms 3 terms call
plot(rf.spotify1)
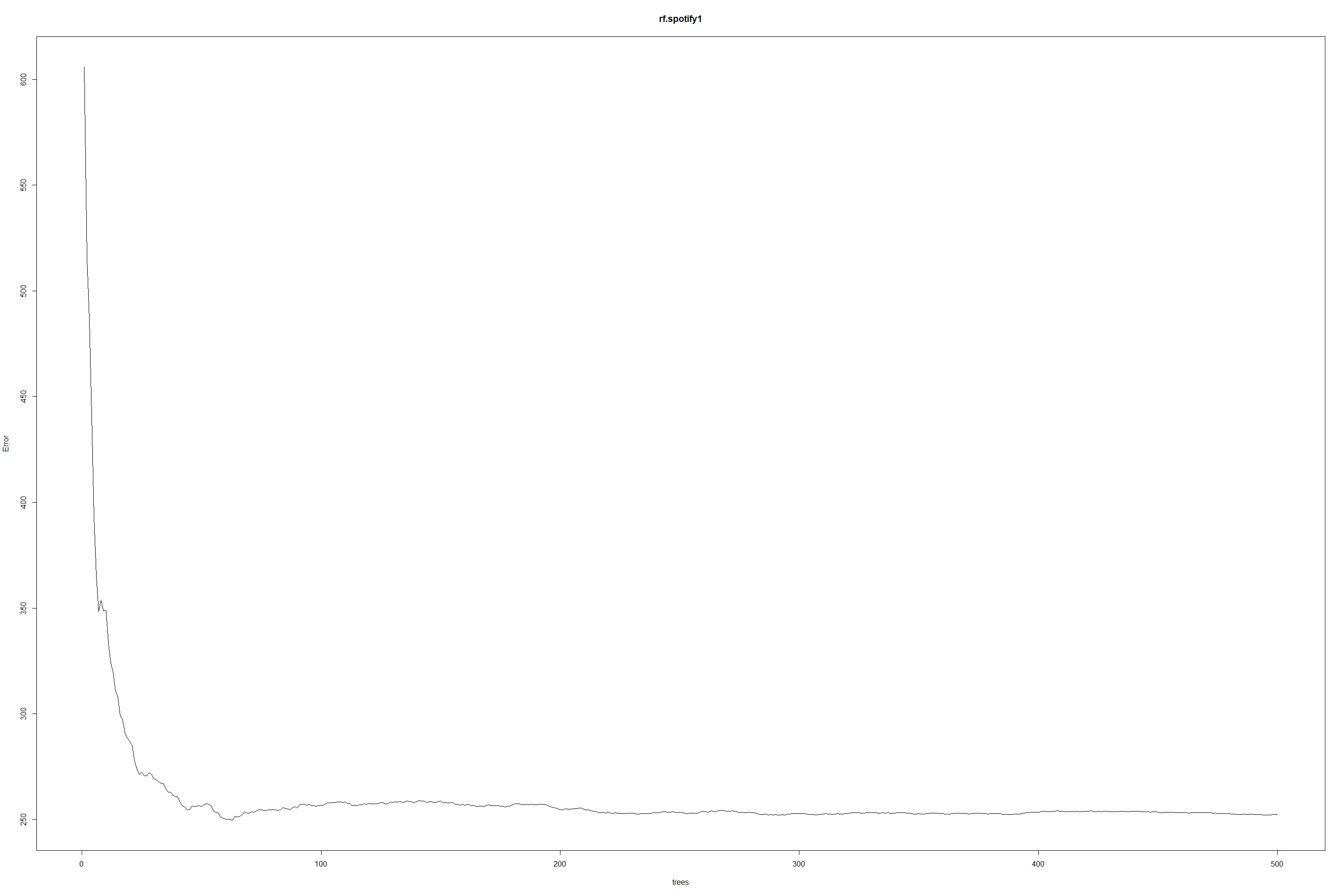
In case of Random Forest regression, number of trees are 500 with 4 variables at each split. as well the MSR is 268 and explained variance is still low 29.36 % of variance explained.
Use Random forest to find Variance based Feature Importances.
rf.spotify1$importance
## %IncMSE IncNodePurity
## acousticness 55.95908992 12605.0567
## danceability 22.03038902 8647.4407
## duration_ms 9.22192386 8241.6846
## energy 42.17450145 12862.5013
## instrumentalness 4.97503172 5337.2879
## key -0.02289204 3735.8114
## liveness 11.30851797 7645.4004
## loudness 80.13705716 17885.1039
## mode 0.17800134 651.4502
## speechiness 17.07094876 9700.8265
## tempo -0.60940613 5763.0800
## valence 21.00623772 9465.7108
rf.spotify1$importanceSD
## acousticness danceability duration_ms energy
## 3.4026817 2.0501844 1.6897903 3.3090501
## instrumentalness key liveness loudness
## 1.4894041 1.1369833 1.6464020 4.1474246
## mode speechiness tempo valence
## 0.5006059 1.9783162 1.4527310 2.0135681
Plot the Feature importances from Random Forest Regression for each feature.
create_rfplot <- function(rf, type){
imp <- importance(rf, type = type, scale = F)
featureImportance <- data.frame(Feature = row.names(imp), Importance = imp[,1])
p <- ggplot(featureImportance, aes(x = reorder(Feature, Importance), y = Importance)) +
geom_bar(stat = "identity", fill = featureImportance$Importance, width = 0.65) +
coord_flip() +
theme_light(base_size = 25) +
theme(axis.title.x = element_text(size = 20, color = "black"),
axis.title.y = element_blank(),
axis.text.x = element_text(size = 20, color = "black"),
axis.text.y = element_text(size = 20, color = "black"))
return(p)
}
create_rfplot(rf.spotify1, type = 2)
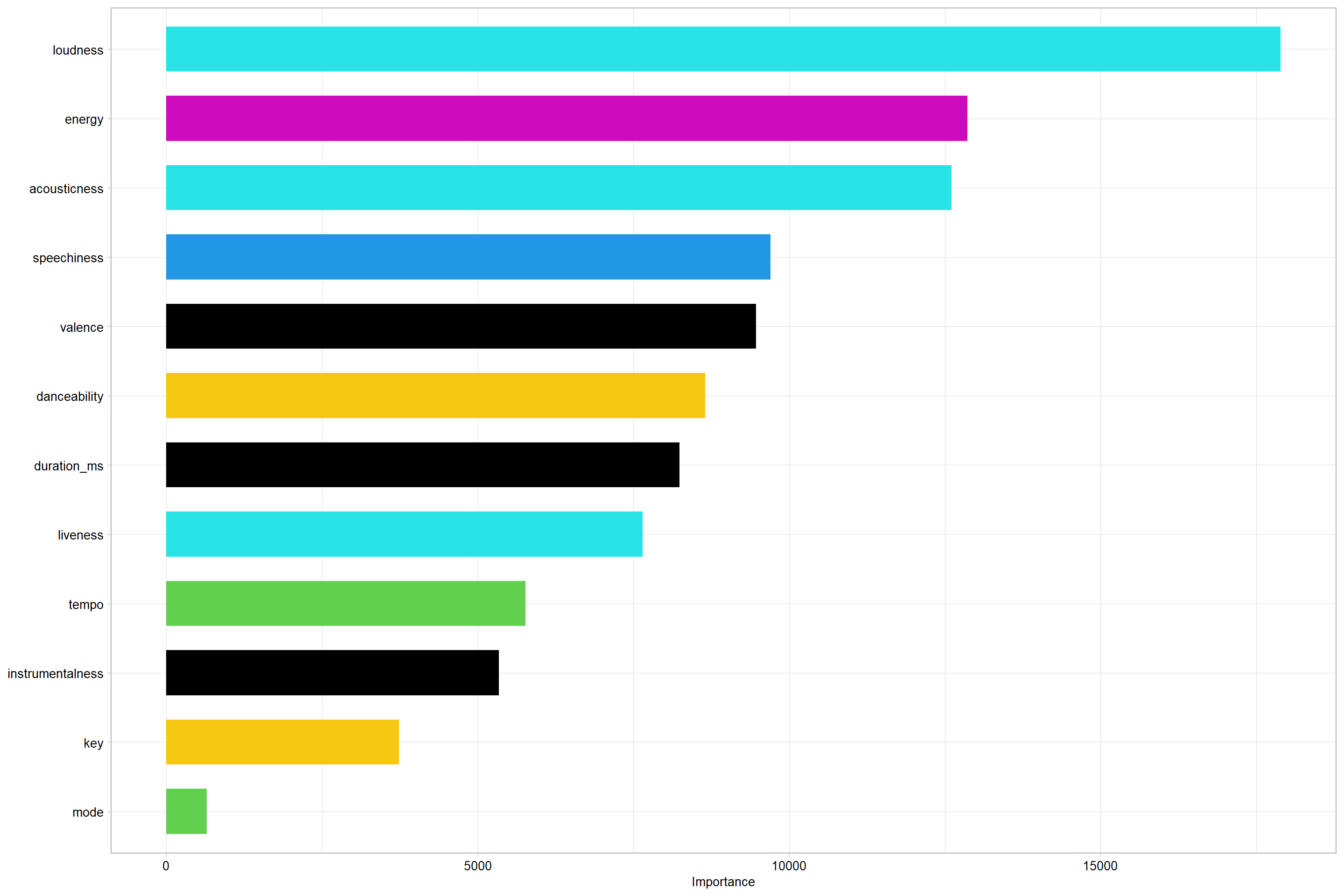
The Random Forest Regression Feature importances suggest that duration is the most important feature of the response variable i.e Popularity score.
data.frame(Feature = row.names(rf.spotify1$importance), Importance = rf.spotify1$importance[,1])
## Feature Importance
## acousticness acousticness 55.95908992
## danceability danceability 22.03038902
## duration_ms duration_ms 9.22192386
## energy energy 42.17450145
## instrumentalness instrumentalness 4.97503172
## key key -0.02289204
## liveness liveness 11.30851797
## loudness loudness 80.13705716
## mode mode 0.17800134
## speechiness speechiness 17.07094876
## tempo tempo -0.60940613
## valence valence 21.00623772
To do permutation Importance to compare Feature importances with that of Feature Importances from Random Forest regression’s variance based importance, we need forest and inbag values to be available in RFR forest object so Permutation-based analysis over repeated samples of all-features-except-one is done based on available statistical information. This makes Permutation Importance more relevant. The Permutation Importance done here is also conditional since we observe multi-collinearity between predictors/independent features themselves. Conditional Permutation importance more relevant in this case since finding accuracy when correlation threshold is (suggested > 0.2) which is true in this case. We have multiple features having correlation > 0.2 suggesting Conditional Permutation Importance as more appropriate method to find importance of a feature’s relation to response variable.
rf.spotify2 = randomForest(popularity~., data = numeric_spotifydf, subset = train, replace = FALSE, nodesize = 7, keep.forest = TRUE, keep.inbag = TRUE)
rf.spotify2
##
## Call:
## randomForest(formula = popularity ~ ., data = numeric_spotifydf, replace = FALSE, nodesize = 7, keep.forest = TRUE, keep.inbag = TRUE, subset = train)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 4
##
## Mean of squared residuals: 252.8918
## % Var explained: 29.7
permimp <- permimp(rf.spotify2, conditional = TRUE, progressBar = FALSE, do_check=FALSE)
Permutation Importances
Permutation Importances are calculated by repeated bagging, bootstrapping and sampling from Random Forest Regression fit to derive importance of a feature based on change in error (positive or negative or none). If there was no change in error in absence of a feature, that feature is considered not important for observed values of reponse variable.
permimp$values
## acousticness danceability duration_ms energy
## 5.3470576 3.6008010 7.2297653 4.0697142
## instrumentalness key liveness loudness
## 1.9339750 -0.5066263 7.7201003 6.5842309
## mode speechiness tempo valence
## -0.3947914 7.3091028 -1.3946197 10.0170245
ggplot(as.data.frame(permimp$values), aes(x = reorder(names(permimp$values)
, as.numeric(permimp$values)), y = as.numeric(permimp$values))) +
geom_bar(stat = "identity", fill = as.factor(seq(0,11)), width = 0.65) +
coord_flip() +
theme_light(base_size = 25) +
theme(axis.title.x = element_text(size = 20, color = "black"),
axis.title.y = element_blank(),
axis.text.x = element_text(size = 20, color = "black"),
axis.text.y = element_text(size = 20, color = "black"))+xlab("Features")+ylab("Importance")
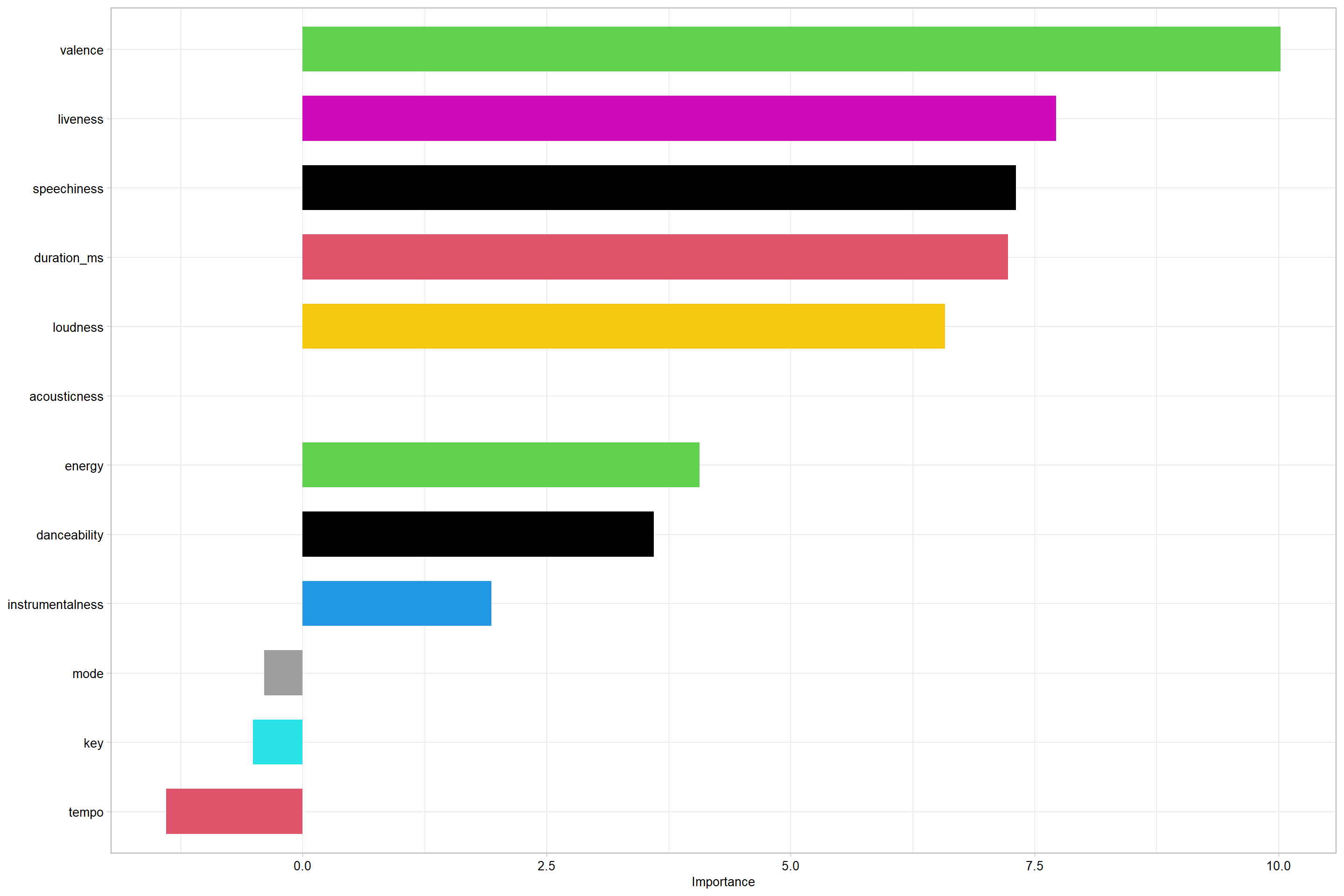
Lastly, we see that on the contrary, acousticness has no influence over popularity score. However, duration, instrumentalness, loudness, valence seem to have good influence over response variable.
Finally, we think given the number of tracks, we can use most statsitically important features to train and test regression fit using cross validation and epochs. Further we would like to conduct tests on a randomly generated date from the model fit. We further would like to explore, as a future work, to find regression or models that better fit multi-collinear features while also finding some better techniques to normalize each of feature-wise distributions.
Potential Bias and Conclusion
Bias
Following are some of the bias affecting our data and causing an unreliable analysis.
-
Currently, the Spotify user base predominantly comprises European, North American and Latin America listenersref. This heavily influences popularity charts and which songs get plays. This lack of diversity certainly affects our data set and makes it less nuanced.
-
There are over 70 million songs on Spotify, of which this data set includes only 230,000. Having feature values of these less popular songs would be immensely helpful to determine which songs have the potential to get famous.
-
On the analytics end, our modest learning models have a limited capability of predicting popularity with the provided variables. We might need to get more sophisticated with our modeling as we have only scratched the surface at this point of time and might need to apply fancier predictive.
-
A more robust dataset with added attributes, in addition to a more elegant model, would definitely prove more effective and help us achieve our end goals with more satisfactory results.
Conclusion
Lastly, we see that on the contrary, acousticness has no influence over
popularity score. However, duration, instrumentalness, loudness, valence
seem to have good influence over response variable.
Finally, we think given the number of tracks, we can use most
statistically important features to train and test regression fit using
cross validation and epochs. Further we would like to conduct tests on a
randomly generated date from the model fit. We further would like to
explore, as a future work, to find regression or models that better fit
multi-collinear features while also finding some better techniques to
normalize each of feature-wise distributions. The additional information
about musical and vocal acoustics and the pattern in which the acoustic
signals themselves relate to the popularity score will be helpful.